中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

設．
（1）求的單調區(qū)間；
（2）求函數(shù)在上的最值．
（1）函數(shù)的單調增區(qū)間是，單調遞減區(qū)間是
（2）最大值是，最小值是
本試題主要是考查了導數(shù)在研究函數(shù)中的運用。
（1）因為依題意得，

定義域是，然后求解，結合二次不等式得到單調區(qū)間。
（2）在第一問的基礎上可知知道極值，然后比較機制和端點值的大小得到結論。
解：依題意得，
…………2分
定義域是         …………3分
（1）   …………5分
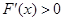
令，得或，
令，得      …………7分
由于定義域是，
函數(shù)的單調增區(qū)間是，單調遞減區(qū)間是…………8分
（2）令，得，…………9分
由于，，，…………11分
在上的最大值是，最小值是…………14分
練習冊系列答案
相關習題

科目：高中數(shù)學 來源：不詳 題型：填空題

設a＞0，若曲線與直線x＝a，y=0所圍成封閉圖形的面積為a，則a =_____.

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

已知，函數(shù)在上為增函數(shù)的概率是（  ）
A．B．C．D．1

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

定積分的值是（　　）
A．B．C．D．

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

若,則的值是(    )
A．2B．3C．4D．6

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

設，則         　.

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

=(    )
A．B．C．D．

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：單選題

＝ 
A．2B．3C．4D．6

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

 _______．

查看答案和解析>>

同步練習冊答案