
(本小題滿分14分)
已知二次函數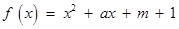 ,關于
,關于 的不等式
的不等式 的解集為
的解集為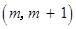 ,其中
,其中 為非零常數.設
為非零常數.設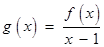 .
.
(1)求 的值;
的值;
(2)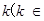 R
R 如何取值時,函數
如何取值時,函數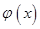
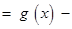
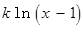 存在極值點,并求出極值點;
存在極值點,并求出極值點;
(3)若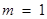 ,且
,且
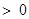 ,求證:
,求證: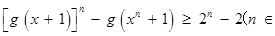 N
N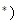
(1)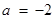 (2)當
(2)當 時,
時,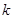 取任意實數, 函數
取任意實數, 函數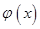 有極小值點
有極小值點 ;
;
當 時,
時,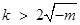 ,函數
,函數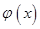 有極小值點
有極小值點 ,有極大值點
,有極大值點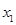 .
.
(其中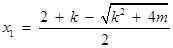 ,
, 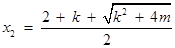 )
)
(3)① 當 時,左邊
時,左邊 ,右邊
,右邊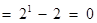 ,不等式成立;② 假設當
,不等式成立;② 假設當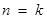
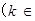 N
N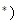 時,不等式成立,即
時,不等式成立,即
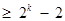 ,
,
則 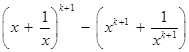
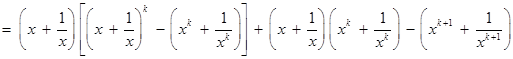
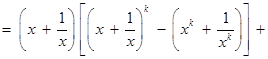

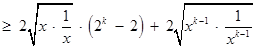
 .
.
也就是說,當 時,不等式也成立.
時,不等式也成立.
由①②可得,對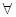
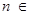 N
N ,
,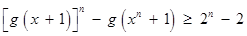 都成立.
都成立.
解析試題分析:(1)解:∵關于 的不等式
的不等式 的解集為
的解集為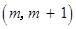 ,
,
即不等式 的解集為
的解集為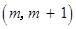 ,
,
∴
 .
.
∴
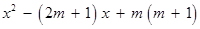 .
.
∴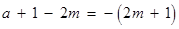 .
.
∴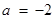 .
.
(2)解法1:由(1)得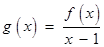
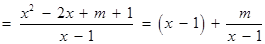 .
.
∴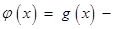
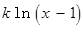
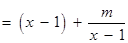
 的定義域為
的定義域為 .
.
∴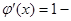
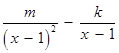
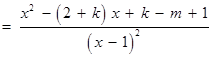 .
.
方程 (*)的判別式
(*)的判別式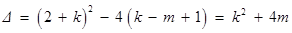 .
.
① 時,
時, ,方程(*)的兩個實根為
,方程(*)的兩個實根為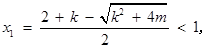

則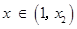 時,
時,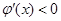 ;
;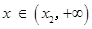 時,
時,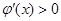 .
.
∴函數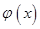 在
在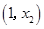 上單調遞減,在
上單調遞減,在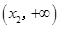 上單調遞增.
上單調遞增.
∴函數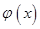 有極小值點
有極小值點 .
.
②當 時,由
時,由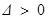 ,得
,得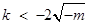 或
或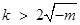 ,
,
若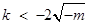 ,則
,則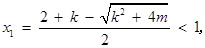
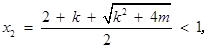
故
 時,
時,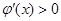 ,
,
∴函數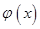 在
在 上單調遞增.
上單調遞增.
∴函數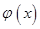 沒有極值點.
沒有極值點.
若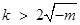 時,
時,
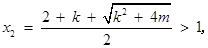
則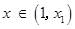 時,
時,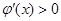 ;
;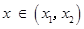 時,
時,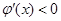 ;
;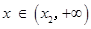 時,
時,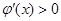 .
.
∴函數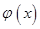 在
在 上單調遞增,在
上單調遞增,在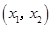 上單調遞減,在
上單調遞減,在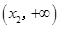 上單調遞增.
上單調遞增.
∴函數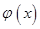 有極小值點
有極小值點 ,有極大值點
,有極大值點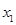 .
.
綜上所述, 當 時,
時,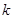 取任意實數, 函數
取任意實數, 函數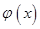 有極小值點
有極小值點 ;
;
當 時,
時,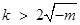 ,函數
,函數


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:解答題
已知x1、x2是關于x的一元二次方程x2+(3a-1)x+2a2-1=0的兩個實數根,使得
(3x1-x2)(x1-3x2)=-80成立.求實數a的所有可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某售報亭每天以每份0.4元的價格從報社購進若干份報紙,然后以每份1元的價格出售,如果當天賣不完,剩下的報紙以每份0.1元的價格賣給廢品收購站.
(Ⅰ)若售報亭一天購進270份報紙,求當天的利潤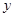 (單位:元)關于當天需求量
(單位:元)關于當天需求量 (單位:份,
(單位:份,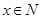 )的函數解析式.
)的函數解析式.
(Ⅱ)售報亭記錄了100天報紙的日需求量(單位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
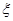 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求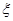 的數學期望;
的數學期望;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分13分)一艘輪船在航行中每小時的燃料費和它的速度的立方成正比,已知在速度為每小時10公里時的燃料費是每小時8元,而其他與速度無關的費用是每小時128元.
(1)求輪船航行一小時的總費用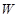 與它的航行速度
與它的航行速度 (公里/小時)的函數關系式;
(公里/小時)的函數關系式;
(2)問此輪船以多大的速度航行時,能使每公里的總費用最少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)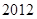 年中秋、國慶長假期間,由于國家實行
年中秋、國慶長假期間,由于國家實行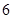 座及以下小型車輛高速公路免費政策,導致在長假期間高速公路出現擁堵現象。長假過后,據有關數據顯示,某高速收費路口從上午
座及以下小型車輛高速公路免費政策,導致在長假期間高速公路出現擁堵現象。長假過后,據有關數據顯示,某高速收費路口從上午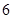 點到中午
點到中午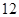 點,車輛通過該收費站的用時
點,車輛通過該收費站的用時 (分鐘)與車輛到達該收費站的時刻
(分鐘)與車輛到達該收費站的時刻 之間的函數關系式可近似地用以下函數給出:
之間的函數關系式可近似地用以下函數給出:
y=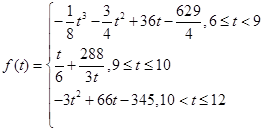
求從上午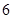 點到中午
點到中午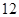 點,通過該收費站用時最多的時刻。
點,通過該收費站用時最多的時刻。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某服裝廠某年1月份、2月份、3月份分別生產某名牌衣服1萬件、 萬件、
萬件、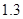 萬件,為了估測當年每個月的產量,以這三個月的產品數量為依據,用一個函數模型模擬該產品的月產量
萬件,為了估測當年每個月的產量,以這三個月的產品數量為依據,用一個函數模型模擬該產品的月產量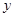 與月份
與月份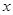 的關系,模擬函數可選用函數
的關系,模擬函數可選用函數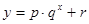 (其中
(其中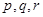 為常數)或二次函數。又已知當年4月份該產品的產量為
為常數)或二次函數。又已知當年4月份該產品的產量為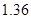 萬件,請問用以上哪個函數作為模擬函數較好,并說明理由。
萬件,請問用以上哪個函數作為模擬函數較好,并說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com