
(1)求函數y=f(x)的表達式;
(2)若g(x)在點(3,g(3))處的切線與直線7x-18y+3=0平行,求函數g(x)的極值;
(3)若函數g(x)在(0,2)上單調遞減,求實數a的取值范圍.
(文)已知A、B、C是直線l上的三點,且滿足:![]() -(y+ax2)
-(y+ax2)![]() +(x3+3x)
+(x3+3x)![]() =0.
=0.
(1)若f(x)在點(1,f(3))處的切線與直線2x+y+3=0平行,求函數y=f(x)的極值;
(2)若函數y=f(x)在(-2,![]() )上單調遞減,求實數口的取值范圍.
)上單調遞減,求實數口的取值范圍.
答案:(理)(1)∵![]() -[y+2f′(1)]
-[y+2f′(1)]![]() +ln(x+1)
+ln(x+1)![]() =0,
=0,
∴![]() =[y+2f′(1)]
=[y+2f′(1)]![]() -ln(x+1)
-ln(x+1)![]()
由于A、B、C三點共線,即[y+2f′(1)]+[-ln(x+1)]=1
∴y=f(x)=ln(x+1)+1-2f′(1)
f′(x)=![]() ,得f′(1)=
,得f′(1)=![]() ,故f(x)=ln(x+1).
,故f(x)=ln(x+1).
(2)∵g(x)=![]() +aln(x+1),
+aln(x+1),
∴g′(x)=![]() ,
,
又x∈(-1,0)∪(0,+∞)
由g′(3)=![]() ,解得a=2
,解得a=2
則g′(x)=![]()
由g′(x)>0解得-1<x<![]() 或x>1,由g′(x)<0
或x>1,由g′(x)<0
解得![]() <x<1
<x<1
則g(x)的增區間是(-1,![]() ),(1,+∞)
),(1,+∞)
g(x)的減區間是(![]() ,0),(0,1)
,0),(0,1)
故g極大值(x)=g(![]() )=-2-ln2,
)=-2-ln2,
g極小值(x)=g(1)=1+21n2.
(3)由g′(x)=![]() <0,得ax2-x-1<0,即a<
<0,得ax2-x-1<0,即a<![]() 在(0,2)上恒成立,
在(0,2)上恒成立,
令u=![]() ,
,
則u在t=![]() ∈(
∈(![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
∴u的最小值趨向于(![]() )2
)2![]() ,但取不到此值
,但取不到此值
∴a≤![]() .
.
(文)∵![]() -(y+ax2)
-(y+ax2)![]() +(x3+3x)
+(x3+3x)![]() =0,
=0,
∴![]() =(y+ax2)
=(y+ax2)![]() -(x3+3x)
-(x3+3x)![]()
由于A、B、C三點共線,得y+ax2-x3=1,即y=x3-ax2+3x+1.
(1)∵f′(x)=3x2-2ax+3,則f′(1)=3x2-2ax+3=3-2a+3=-2,得a=4,
∴f′(x)=3x2-8x+3=3(x-3)(x![]() ),
),
由f′(x)>0解得x<![]() 或x>3;
或x>3;
由f′(x)<0解得![]() <x<3.
<x<3.
則f(x)的增區間是(-∞,![]() ),(3,+∞);減區間是(
),(3,+∞);減區間是(![]() ,3)
,3)
故f極大值(x)=f(![]() )=
)=![]() ,f極小值(x)=f(3)=1.
,f極小值(x)=f(3)=1.
(2)∵f′(x)=3x2-2ax+3,
又f(x)在(-2,![]() )上單調遞減,
)上單調遞減,
∴f′(x)=3x2-2ax+3<0在(-2,![]() )上恒成立f′(x)max<0.
)上恒成立f′(x)max<0.
又∵f′(x)是開口向上的拋物線,
∴只要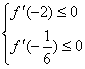 ,即
,即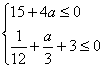 ,
,
解得a≤![]() .
.


科目:高中數學 來源: 題型:
(08年山東卷理)已知a,b,c為△ABC的三個內角A,B,C的對邊,向量m=(![]() ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,則角B=
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,則角B=
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求角C;
(2)求a、b的值.
(文)在△ABC中,sinA+cosA=![]() ,AC=2,AB=3.
,AC=2,AB=3.
(1)求tanA的值;
(2)求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年南寧二中理)已知A、B、C三點共線,且A(3,![]() ),B(
),B(![]() ,2),若C點的橫坐標為6,則C點的縱坐標為 ( )
,2),若C點的橫坐標為6,則C點的縱坐標為 ( )
A.-13 B.9 C.13 D.9
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com