Question

解答下列各題：

(1)已知扇形的周長為10cm，面積為4cm²，求扇形圓心角的弧度數．

(2)已知一扇形的圓心角是72°，半徑等于20cm，求扇形的面積．

(3)已知一扇形的周長為40cm，求它的半徑和圓心角取什么值時，才能使扇形的面積最大？最大面積是多少？

 

Answer 1

【答案】

（1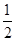） (2) 80π(3) 2, 最大值為100cm²

【解析】(1)設扇形圓心角的弧度數為θ(0<θ<

2π)，弧長為l，半徑為r，

依題意有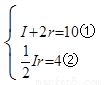

①代入②得r²－5r＋4＝0，解之得r₁＝1，r₂＝4.

當r＝1時，l＝8(cm)，此時，θ＝8rad>2πrad舍去．

當r＝4時，l＝2(cm)，此時，θ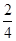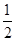＝＝rad.

(2)設扇形弧長為l，∵72°＝72×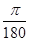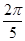＝ (rad)，

∴l＝αR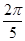＝×20＝8π(cm)．

∴S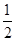＝lR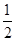＝×8π×20＝80π(cm²)．

(3)設扇形的圓心角為θ，半徑為r，弧長為l，面積為S，則l＋2r＝40，

∴l＝40－2r，∴S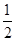＝lr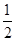＝×(40－2r)r＝(20－r)r＝－(r－10)²＋100.

∴當半徑r＝10cm時，扇形的面積最大．

這個最大值為100cm²，這時θ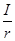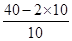＝＝＝2rad.