
已知向量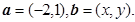
(1)若 分別表示將一枚質地均勻的骰子先后拋擲兩次時第一次、第二次正面朝上出現的點數,求滿足
分別表示將一枚質地均勻的骰子先后拋擲兩次時第一次、第二次正面朝上出現的點數,求滿足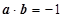 的概率.
的概率.
(2)若 在連續區間[1,6]上取值,求滿足
在連續區間[1,6]上取值,求滿足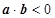 的概率.
的概率.
(1)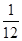 ;(2)
;(2)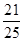 .
.
【解析】
試題分析:(1)擲一枚骰子的結果有6種,先后拋擲兩次,所包含的基本事件總數為6×6=36個,由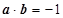 得
得 ,所以
,所以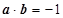 所包含的基本事件為
所包含的基本事件為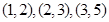 ,所求的概率為
,所求的概率為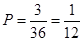 .
.
(2)若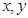 在連續區間[1,6]上取值,這符合幾何概型的條件,事件的全部結果構成的區域
在連續區間[1,6]上取值,這符合幾何概型的條件,事件的全部結果構成的區域
Ω={(x,y)|1≤x≤6,1≤y≤6},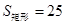 ,滿足
,滿足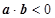 基本事件的結果為
基本事件的結果為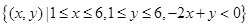 ,
,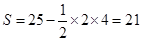 ,所求概率
,所求概率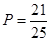 .
.
試題解析:(1)將一枚質地均勻的正方體骰子先后拋擲兩次,所包含的基本事件總數為6×6=36個;由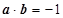 有-2x+y=-1,所以滿足
有-2x+y=-1,所以滿足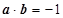 的基本事件為(1,1),(2,3),(3,5),共3個;故滿足
的基本事件為(1,1),(2,3),(3,5),共3個;故滿足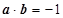 的概率為
的概率為 =
=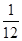 .
.
(2)若x,y在連續區間[1,6]上取值,則全部基本事件的結果為Ω={(x,y)|1≤x≤6,1≤y≤6};滿足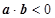 的基本事件的結果為A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};畫出圖形如下圖,
的基本事件的結果為A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};畫出圖形如下圖,
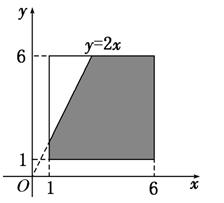
矩形的面積為S矩形=25,陰影部分的面積為S陰影=25-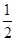 ×2×4=21,
×2×4=21,
故滿足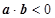 的概率為
的概率為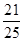 .
.
考點:1、古典概型的求法;2、幾何概型的求法.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數學 來源:河北省冀州中學2010-2011學年高一下學期期末考試數學理科試題(A卷) 題型:044
已知向量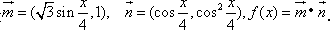
(1)若f(x)=1,求cos(![]() +x)的值;
+x)的值;
(2)在△ABC中,角A、B、C的對邊分別是a、b、c,且滿足(2a-c)cosB=bcosC,求函數f(A)的取值范圍.
查看答案和解析>>
科目:高中數學 來源:安徽省望江縣2012屆高三第一次月考數學理科試題 題型:044
已知向量![]()
(1)若![]() ,求
,求![]() 的值;
的值;
(2)記![]() ,在△ABC中,角A,B,C的對邊分別是a,b,c,且滿足(2a-c)cosB=bcosC,求函數f(A)的取值范圍.
,在△ABC中,角A,B,C的對邊分別是a,b,c,且滿足(2a-c)cosB=bcosC,求函數f(A)的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com