
(本題滿分15分)
為了保護環境,發展低碳經濟,某單位在國家科研部門的支持下,采用了新工藝,把二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理量最少為400噸,最多為600噸,月處理成本 (元)與月處理量
(元)與月處理量 (噸)之間的函數關系可近似的表示為:
(噸)之間的函數關系可近似的表示為: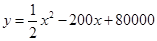 ,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
(1)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則國家至少需要補貼多少元才能使該單位不虧損?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
(本題滿分13分)某工廠有214名工人, 現要生產1500件產品, 每件產品由3個A型零件與1個B型零件配套組成, 每個工人加工5個A型零件與3個B型零件所需時間相同. 現將全部工人分為兩組, 分別加工一種零件, 同時開始加工. 設加工A型零件的工人有x人, 在單位時間內每人加工A型零件5k個(k∈N*), 加工完A型零件所需時間為g(x), 加工完B型零件所需時間為h (x).
(Ⅰ) 試比較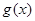 與
與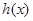 大小, 并寫出完成總任務的時間
大小, 并寫出完成總任務的時間 的表達式;
的表達式;
(Ⅱ) 怎樣分組才能使完成任務所需時間最少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某產品生產廠家根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品x(百臺),其總成本為G(x)(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本).銷售收入R(x)(萬元)滿足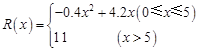 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
(1)寫出利潤函數y=f(x)的解析式(利潤=銷售收入-總成本);
(2)工廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分16分)
已知 ,
,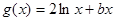 ,且直線
,且直線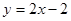 與曲線
與曲線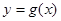 相切.
相切.
(1)若對 內的一切實數
內的一切實數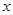 ,不等式
,不等式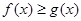 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍;
(2)當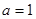 時,求最大的正整數
時,求最大的正整數 ,使得對
,使得對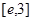 (
(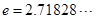 是自然對數的底數)內的任意
是自然對數的底數)內的任意 個實數
個實數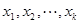 都有
都有 成立;
成立;
(3)求證: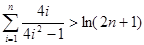
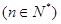 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
我市有甲、乙兩家乒乓球俱樂部,兩家設備和服務都很好,但收費方式不同.甲家每張球臺每小時5元;乙家按月計費,一個月中30小時以內(含30小時)每張球臺90元,超過30小時的部分每張球臺每小時2元.小張準備下個月從這兩家中的一家租一張球臺開展活動,其活動時間不少于15小時,也不超過40小時.
(1)設在甲家租一張球臺開展活動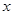 小時的收費為
小時的收費為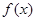 元
元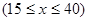 ,在乙家租一張球臺開展活動
,在乙家租一張球臺開展活動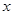 小時的收費為
小時的收費為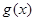 元
元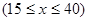 ,試求
,試求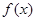 和
和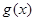 。
。
(2)問:小張選擇哪家比較合算?說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com