
某校高一某班的一次數學測試成績(滿分100分)的莖葉圖和頻率分布直方圖都受到不同程度的污染,但可見部分如下,據此解答如下問題:
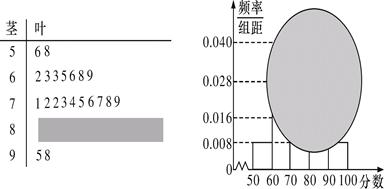
(Ⅰ) 求分數在[50,60)的頻率及全班人數;
(Ⅱ) 求分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(Ⅲ)若要從分數在[80,100]之間的試卷中任取兩份分析學生失分情況,在抽取的試卷中,求至少有一份分數在[90,100]之間的概率.
(Ⅰ)分數在[50,60)之間的頻數為2,所以全班人數為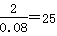 , (Ⅱ) 0.016,(Ⅲ) 0.6
, (Ⅱ) 0.016,(Ⅲ) 0.6
【解析】
試題分析:(Ⅰ) 分數在[50,60)的頻率為0.008×10=0.08,
由莖葉圖知:分數在[50,60)之間的頻數為2,所以全班人數為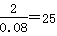 , 3分
, 3分
(Ⅱ) 分數在[80,90)之間的頻數為25-2-7-10-2=4;
頻率分布直方圖中[80,90)間的矩形的高為 .
6分
.
6分
(Ⅲ)將[80,90)之間的4個分數編號為1,2,3,4,[90,100]之間的2個分數編號為5,6,
在[80,100]之間的試卷中任取兩份的基本事件為:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6)共15個,
其中,至少有一個在[90,100]之間的基本事件有9個,
故至少有一份分數在[90,100]之間的概率是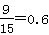 12分
12分
考點:本題考查了頻率分布直方圖的運用及古典概型的求法
點評:注意頻率分布直方圖中用小長方形面積的大小來表示在各個區間內取值的頻率,所以在求面積時,通過已知求出所要區間的面積即可


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
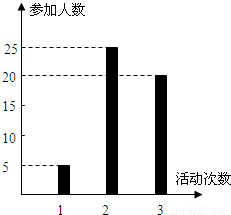
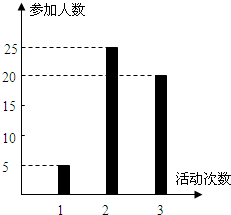 按照新課程的要求,高中學生在每學期都要至少參加一次社會實踐活動(以下簡稱活動).某校高一•一班50名學生在上學期參加活動的次數統計如條形圖所示.
按照新課程的要求,高中學生在每學期都要至少參加一次社會實踐活動(以下簡稱活動).某校高一•一班50名學生在上學期參加活動的次數統計如條形圖所示.. | x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:2010年吉林省高三第五次模擬考試數學(理科)試題 題型:解答題
(本小題滿分12分)
按照新課程的要求, 高中學生在每學期都要至少參加一次社會實踐活動(以下簡稱活動).某校高一·一班50名學生在上學期參加活動的次數統計如條形圖所示.
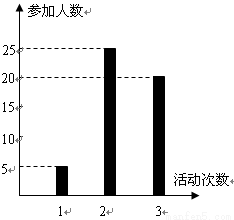
(Ⅰ)求該班學生參加活動的人均次數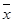 ;
;
(Ⅱ)從該班中任意選兩名學生,求他們參加活動次數恰好相等的概率;
(Ⅲ)從該班中任選兩名學生,用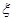 表示這兩人參加活動次數之差的絕對值,求隨機變量
表示這兩人參加活動次數之差的絕對值,求隨機變量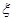 的分布列及數學期望
的分布列及數學期望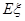 .(要求:答案用最簡分數表示)
.(要求:答案用最簡分數表示)
查看答案和解析>>
科目:高中數學 來源:2010年吉林省長春市東北師大附中高考數學五模試卷(理科)(解析版) 題型:解答題
 ;
;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com