
在邊長為a的正方形ABCD所在平面外取一點P,使PA⊥平面ABCD,且PA=AB,在AC的延長線上取一點G。
(1)若CG=AC,求異面直線PG與CD所成角的大小;
(2)若CG=AC,求點C到平面PBG的距離;
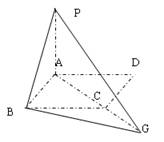
(3)當點G在AC的延長線上運動時(不含端點C),求二面角P-BG-C的取值范圍。
(1)![]() (2)
(2)![]() (3)二面角P-BG-C的取值范圍是
(3)二面角P-BG-C的取值范圍是![]()
分析:本題如利用“幾何法”,則通過“平移變換”將異面直線角化歸為三角形的內角,由解三角形的方法求之,凡“點面距離”可利用等積法求之,至于二面角,則通過“作-證-算”三步曲求得;本題如利用“向量法”,則建立適當的空間直角坐標系,寫出各點坐標,再根據公式而求之。
方法一:(1)過點G作GE∥CD交AD的延長線于點E,連PE,則∠PGE是異面直線PG與CD所成的角,,則由條件得GE=2a,PG=3a,
cos ∠PGE=![]() ,所以異面直線PG與CD所成角等于
,所以異面直線PG與CD所成角等于![]() ;
;
(2)設h,則利用等積法知![]() ,在△PBG中,PB=
,在△PBG中,PB=![]() ,PG=3a,BG=
,PG=3a,BG=![]() ,
,![]() ,得
,得![]() ,又在△CBG中,
,又在△CBG中,![]() ,從而由
,從而由![]() 得
得![]() ;
;
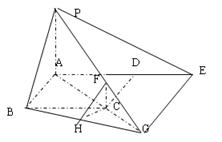
(3)作CF⊥AC交PG于F,作FH⊥BG交BG于H,連CH,因為PA⊥平面ABCD,所以PA⊥AC,所以PA∥CG,得CG⊥平面ABCD,由三垂線定理得∠FHC是二面角P-BG-C的平面角,設![]() ,則由△CGF∽△AGP得
,則由△CGF∽△AGP得![]() ,
,
在△CBG中![]() ,得
,得![]()
所以![]() ,從而
,從而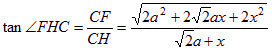
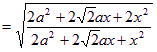
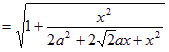
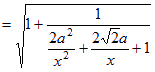
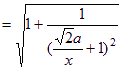
![]() ,所以二面角P-BG-C的取值范圍是
,所以二面角P-BG-C的取值范圍是![]() 。
。
方法二:建立如圖所示的直角坐標系,
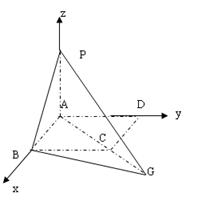
則A(0,0,O、0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,a)。
由條件得G(2 a ,2 a ,0),
![]() ,
,![]()
所以![]() ,
,
所以異面直線PG與CD所成角等于![]() ;
;
(2)設平面PBG的法向量為![]() 因
因![]() ,
,![]()
所以由![]() 得
得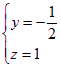 ,即
,即![]() 又
又![]() ,
,
所以點C到平面PBG的距離為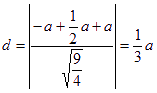 ;
;
由條件設G(t,t,0), 其中![]() ,平面PBG的法向量為
,平面PBG的法向量為![]()
因![]() ,
,![]() ,所以由
,所以由![]() 得
得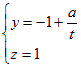 ,
,
即![]() 而平面CBG的法向量
而平面CBG的法向量![]() ,
,
所以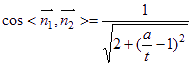 ,因為
,因為![]() ,所以
,所以![]() ,
,
易知二面角P-BG-C的平面角是銳角,所以二面角P-BG-C的平面角等于![]() ,所以二面角PP-BG-C的取值范圍是
,所以二面角PP-BG-C的取值范圍是![]() 。
。
點評:本題主要考查異面直線所成角的空間想象能力,利用體積法求點面距離的運算能力,二面角的估算能力,第(3)問有機的將函數的值域與立體幾何結合,較好地考查學生綜合分析與解決問題的能力.


科目:高中數學 來源: 題型:
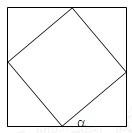 在邊長為a的正方形ABCD中內依次作內接正方形AiBiCiDi(i=1,2,3,…),使內接正方形與相鄰前一個正方形的一邊夾角為a,求所有正方形的面積之和.
在邊長為a的正方形ABCD中內依次作內接正方形AiBiCiDi(i=1,2,3,…),使內接正方形與相鄰前一個正方形的一邊夾角為a,求所有正方形的面積之和.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,在邊長為a的正方形組成的網格中,設橢圓C1、C2、C3的離心率分別為e1、e2、e3,則e1、e2、e3的關系為
如圖所示,在邊長為a的正方形組成的網格中,設橢圓C1、C2、C3的離心率分別為e1、e2、e3,則e1、e2、e3的關系為查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•海淀區二模)如圖,在邊長為a的正方形內有不規則圖形Ω.向正方形內隨機撒豆子,若撒在圖形Ω內和正方形內的豆子數分別為m,n,則圖形Ω面積的估計值為( )
(2013•海淀區二模)如圖,在邊長為a的正方形內有不規則圖形Ω.向正方形內隨機撒豆子,若撒在圖形Ω內和正方形內的豆子數分別為m,n,則圖形Ω面積的估計值為( )
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在邊長為a的正方形ABCD中內依次作內接正方形AiBiCiDi(i=1,2,3,…),使內接正方形與相鄰前一個正方形的一邊夾角為a,求所有正方形的面積之和.
在邊長為a的正方形ABCD中內依次作內接正方形AiBiCiDi(i=1,2,3,…),使內接正方形與相鄰前一個正方形的一邊夾角為a,求所有正方形的面積之和.查看答案和解析>>
科目:高中數學 來源:高考數學一輪復習必備(第92-93課時):第十二章 極限-數列的極限、數學歸納法(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com