
使得函數(shù)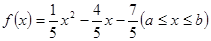 的值域為
的值域為 的實數(shù)對
的實數(shù)對
有( )對
| A.1 | B.2 | C.3 | D.無數(shù) |
B
解析試題分析: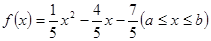 為開口向上的拋物線,所以x在[2,+∞)上單調(diào)遞增,在(-∞,2]上單調(diào)遞減
為開口向上的拋物線,所以x在[2,+∞)上單調(diào)遞增,在(-∞,2]上單調(diào)遞減
(1) 2≤a<b,此時[a,b]在f(x)的單調(diào)增區(qū)間上則最大值b=f(b),最小值a=f(a),即a、b為方程x=f(x)的兩根。
x=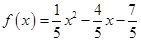 ,即
,即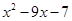 =0的兩根為a、b,
=0的兩根為a、b,
由韋達定理,ab=-7,即a、b異號,這與0<2<a<b矛盾,所以這種情況不可能。
(2) a<b≤2,此時[a,b]在f(x)的單調(diào)減區(qū)間上,
則最大值b=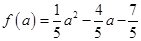 ①,最小值a=
①,最小值a=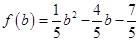 ②
②
由①-②,得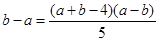 ,
,
由于a<b,所以a-b≠0,可得-1=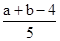 ,a+b=-1可得a=-1-b,將其代入①,得
,a+b=-1可得a=-1-b,將其代入①,得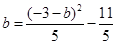 且b=-1-a,將其代入②,的
且b=-1-a,將其代入②,的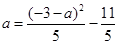 , 則a、b為方程
, 則a、b為方程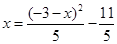 的兩根,
的兩根,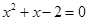 ,解得x=1,-2,由于a<b,所以a=-2,b=1,滿足a<b≤2,所以(a,b)=(-2,1)是一組解。
,解得x=1,-2,由于a<b,所以a=-2,b=1,滿足a<b≤2,所以(a,b)=(-2,1)是一組解。
(3) a<2<b,此時[a,b]包含x=2
則最小值a=f(2)=-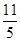 ,滿足a<2,而f(x)在[a,2]上單調(diào)減,在[2,b]上單調(diào)增
,滿足a<2,而f(x)在[a,2]上單調(diào)減,在[2,b]上單調(diào)增
所以最大值為f(a)或f(b),最大值須進一步分類討論:
注意到|a-2|=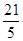 ,所以進行如下分類:
,所以進行如下分類:
1° |b-2|>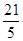 ,即b>
,即b>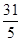
此時由于|b-2|>|a-2|,f(b)= 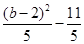 >f(a)=
>f(a)= 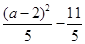 即最大值,
即最大值,
b="f(b)=" 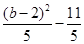 ,
,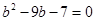 ,解得b=
,解得b=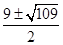 其中b=
其中b=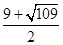 滿足b>
滿足b>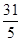 ,
,
所以(a,b)="(" 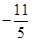 ,
, 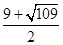 )是另一組解;
)是另一組解;
2° |b-2|<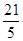 ,即2<b<
,即2<b<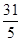 。此時由于|b-2|<|a-2|,
。此時由于|b-2|<|a-2|,
f(b)= 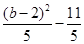 <f(a)=
<f(a)= 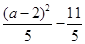 ,
,
即最大值b=f(a)=f(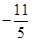 )=
)=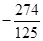 <0,與b>2矛盾,所以這種情況不可能;
<0,與b>2矛盾,所以這種情況不可能;
綜上所述,滿足題意的(a,b)有2對,故選 B.
考點:本題主要考查二次函數(shù)的圖象和性質(zhì),分類討論思想。
點評:難題,涉及二次函數(shù)值域問題,關(guān)注圖象的開口方向、對稱軸位置、區(qū)間端點函數(shù)值,均為基本方法。本題分類討論易于出錯,特別是第三種情況下。


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:高中數(shù)學 來源: 題型:單選題
設(shè)f(x)是以2為周期的奇函數(shù),且f(-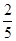 )=3,若sinα=
)=3,若sinα=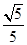 ,則f(4cos2α)= ( )
,則f(4cos2α)= ( )
| A.-3 | B.3 | C.-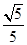 | D.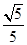 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
已知函數(shù)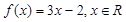 規(guī)定:給出一個實數(shù)
規(guī)定:給出一個實數(shù)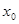 ,賦值
,賦值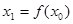 ,若
,若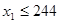 ,則繼續(xù)賦值
,則繼續(xù)賦值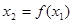 , ,
, , 以此類推,若
以此類推,若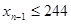 ,則
,則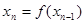 ,否則停止賦值,如果得到
,否則停止賦值,如果得到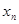 稱為賦值了
稱為賦值了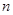 次
次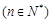 .已知賦值了
.已知賦值了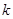 次后停止,則
次后停止,則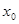 的取值范圍是( )
的取值范圍是( )
A.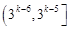 | B.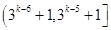 | C.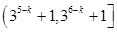 | D.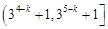 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
已知函數(shù)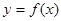 的導函數(shù)
的導函數(shù)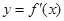 的圖像如下,則( )
的圖像如下,則( )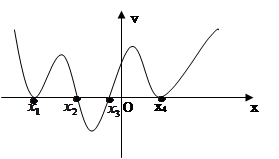
A.函數(shù)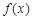 有1個極大值點,1個極小值點 有1個極大值點,1個極小值點 |
B.函數(shù)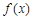 有2個極大值點,2個極小值點 有2個極大值點,2個極小值點 |
C.函數(shù)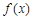 有3個極大值點,1個極小值點 有3個極大值點,1個極小值點 |
D.函數(shù)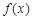 有1個極大值點,3個極小值點 有1個極大值點,3個極小值點 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:單選題
設(shè)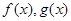 分別是定義在R上的奇函數(shù)和偶函數(shù),當
分別是定義在R上的奇函數(shù)和偶函數(shù),當 時,
時,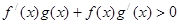 ,且
,且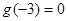 ,則
,則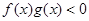 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com