
已知關于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a,b是一枚骰子擲兩次所得到的點數,求方程有兩正根的概率;
(2)若a∈[2,6],b∈[0,4],求方程沒有實根的概率.
(1)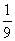 (2)
(2)
解析試題分析:解:(1)基本事件(a,b)共有36個,方程有正根等價于a-2>0,16-b2>0,Δ≥0,
即a>2,-4<b<4,(a-2)2+b2≥16.
設“方程有兩個正根”為事件A,則事件A包含的基本事件為(6,1),(6,2),(6,3),(5,3),共4個,
故所求的概率為P(A)= =
=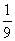 .
.
(2)試驗的全部結果構成區域Ω={(a,b)|2≤a≤6,0≤b≤4},
其面積為S(Ω)=16,
設“方程無實根”為事件B,則構成事件B的區域為
B={(a,b)|2≤a≤6,0≤b≤4,(a-2)2+b2<16},
其面積為S(B)= ×π×42=4π,
×π×42=4π,
故所求的概率為P(B)=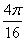 =
=
考點:古典概型的概率
點評:主要是考查了隨機事件的概率的運用,屬于基礎題。


科目:高中數學 來源: 題型:解答題
甲乙兩班進行消防安全知識競賽,每班出3人組成甲乙兩支代表隊,首輪比賽每人一道必答題,答對則為本隊得1分,答錯不答都得0分,已知甲隊3人每人答對的概率分別為 ,乙隊每人答對的概率都是
,乙隊每人答對的概率都是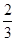 .設每人回答正確與否相互之間沒有影響,用
.設每人回答正確與否相互之間沒有影響,用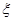 表示甲隊總得分.
表示甲隊總得分.
(I)求隨機變量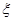 的分布列及其數學期望E(
的分布列及其數學期望E(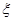 );
);
(Ⅱ)求在甲隊和乙隊得分之和為4的條件下,甲隊比乙隊得分高的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
)袋中裝有大小相同的黑球、白球和紅球共10個。已知從袋中任意摸出1個球,得到黑球的概率是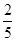 ;從袋中任意摸出2個球,至少得到1個白球的概率是
;從袋中任意摸出2個球,至少得到1個白球的概率是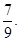
(1)求袋中各色球的個數;
(2)從袋中任意摸出3個球,記得到白球的個數為ξ,求隨機變量ξ的分布列及數學期望Eξ和方差Dξ;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙、丙三人獨立參加某企業的招聘考試,根據三人的專業知識、應試表現、工作經驗等綜合因素,三人被招聘的概率依次為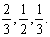 用
用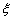 表示被招聘的人數。
表示被招聘的人數。
(1)求三人中至少有一人被招聘的概率;
(2)求隨機變量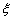 的分布列和數學期望。
的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
將一顆質地均勻的正方體骰子(六個面的點數分別為1,2,3,4,5,6)先后拋擲兩次,將得到的點數分別記為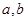 .
.
(1)求直線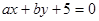 與圓
與圓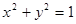 相切的概率;
相切的概率;
(2)將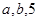 的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
哈爾濱市第一次聯考后,某校對甲、乙兩個文科班的數學考試成績進行分析,規定:大于或等于120分為優秀,120分以下為非優秀.統計成績后,得到如下的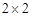 列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為
列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為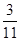 。
。
| | 優秀 | 非優秀 | 合計 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合計 | | | 110 |
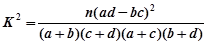 。
。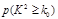 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1)從1,2,3,4,5五個數中依次取2個數,求這兩個數的差的絕對值等于1的概率;
(2)△ABC中,∠B=60°,∠C=45°,高AD=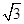 ,在BC邊上任取一點M,求
,在BC邊上任取一點M,求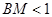 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了保養汽車,維護汽車性能,汽車保養一般都在購車的4S店進行,某地大眾汽車4S店售后服務部設有一個服務窗口專門接待保養預約。假設車主預約保養登記所需的時間互相獨立,且都是整數分鐘,對以往車主預約登記所需的時間統計結果如下:
| 登記所需時間(分) | 1 | 2 | 3 | 4 | 5 |
| 頻率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校設計了一個實驗考查方案:考生從 道備選題中一次性隨機抽取
道備選題中一次性隨機抽取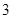 道題,按照題目要求獨立完成全部實驗操作.規定:至少正確完成其中
道題,按照題目要求獨立完成全部實驗操作.規定:至少正確完成其中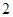 道題的便可通過.已知
道題的便可通過.已知 道備選題中考生甲有
道備選題中考生甲有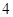 道題能正確完成,
道題能正確完成,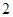 道題不能完成;考生乙每題正確完成的概率都是
道題不能完成;考生乙每題正確完成的概率都是 ,且每題正確完成與否互不影響.
,且每題正確完成與否互不影響.
(1)求甲、乙兩考生正確完成題數的概率分布列,并計算其數學期望;
(2)請分析比較甲、乙兩考生的實驗操作能力.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com