
定義在 上的函數
上的函數 對任意
對任意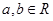 都有
都有 (
(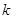 為常數).
為常數).
(1)判斷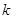 為何值時
為何值時 為奇函數,并證明;
為奇函數,并證明;
(2)設 ,
, 是
是 上的增函數,且
上的增函數,且 ,若不等式
,若不等式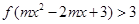 對任意
對任意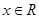 恒成立,求實數
恒成立,求實數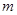 的取值范圍.
的取值范圍.
(1)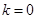 ,證明過程詳見解析;(2)
,證明過程詳見解析;(2)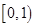 .
.
【解析】
試題分析:本題主要考查抽象函數奇偶性的判斷和利用函數單調性解不等式.考查學生的分析問題解決問題的能力.考查轉化思想和分類討論思想.第一問,用賦值法證明函數的奇偶性;第二問,利用單調性解不等式,轉化成恒成立問題,再利用二次函數的性質求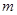 的取值范圍.
的取值范圍.
試題解析:(Ⅰ)若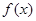 在
在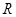 上為奇函數,則
上為奇函數,則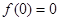 ,
1分
,
1分
令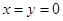 ,則
,則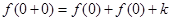 ,∴
,∴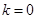 . 2分
. 2分
證明:由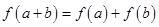 ,令
,令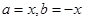 ,則
,則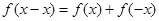 ,
,
又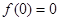 ,則有
,則有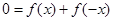 .即
.即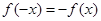 對任意
對任意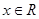 成立,所以
成立,所以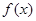 是奇函數.
是奇函數.
6分
(Ⅱ)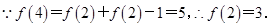 7分
7分
∴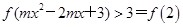 對任意
對任意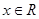 恒成立.
恒成立.
又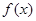 是
是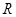 上的增函數,∴
上的增函數,∴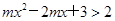 對任意
對任意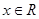 恒成立, 9分
恒成立, 9分
即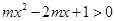 對任意
對任意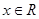 恒成立,
恒成立,
當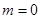 時顯然成立;
時顯然成立;
當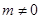 時,由
時,由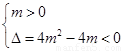 得
得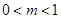 .
.
所以實數m的取值范圍是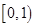 . 13分
. 13分
考點:1.抽象函數的奇偶性的判斷;2.恒成立問題.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com