中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

函數y = 1n|x－1|的圖像與函數y="-2" cos 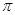x（-2≤x≤4）的圖像所有交點的橫坐標之和等于

A．8                B．6                C．4                D．2

 

【答案】

B

【解析】

試題分析：在同一平面直角坐標系中，畫出函數y = 1n|x－1|的圖像與函數y="-2" cos x（-2≤x≤4）的圖像，易知函數y = 1n|x－1|的圖像與函數y="-2" cos x（-2≤x≤4）的圖像都關于直線x=1對稱，且在直線x=1的左右兩側各有3個交點，3個交點都分別關于直線x=1對稱，所以所有交點的橫坐標之和等于6.

考點：對數函數的圖像；三角函數的圖像；圖像的變換；函數的性質；中點坐標公式。

點評：此題主要考查數形結合的數學思想。做此題的關鍵是正確、快速的畫出函數y = 1n|x－1|與函數y="-2" cos x（-2≤x≤4）的圖像。屬于中檔題。

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設函數y=f（x）滿足對任意x1、x2∈R都有f（x1+x2）=f（x1）f（x2），且f（1）=2．
（Ⅰ）求f（2）、f（3）、f（4），猜測一個計算f（n）（n∈N*）的公式（不要求證明）；
（Ⅱ）設an=
log2f(
1
n
)
(n=1，2，3，…)，
（1）證明：a1+a2+a3＞2；
（2）證明：a1+a2+a3+…+an＜2
n
(n∈N*)．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知函數f（x）=lnax-
x-a
x
（a≠0）
（Ⅰ）求此函數的單調區間及最值
（Ⅱ）求證：對于任意正整數n均有1+
1
2
+
1
3
+…+
1
n
≥
1
2
ln
(2e)2
n!
，其中e為自然對數的底數；
（Ⅲ）當a=1時，是否存在過點（1，-1）的直線與函數y=f（x）的圖象相切？若存在，有多少條？若不存在，說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•江西）若函數h（x）滿足
①h（0）=1，h（1）=0；
②對任意a∈[0，1]，有h（h（a））=a；
③在（0，1）上單調遞減．則稱h（x）為補函數．已知函數h（x）=(
1-xp
1+λxp
)
1
p
（λ＞-1，p＞0）
（1）判函數h（x）是否為補函數，并證明你的結論；
（2）若存在m∈[0，1]，使得h（m）=m，若m是函數h（x）的中介元，記p=
1
n
（n∈N+）時h（x）的中介元為xn，且Sn=
n
i=1
xi，若對任意的n∈N+，都有Sn＜
1
2
，求λ的取值范圍；
（3）當λ=0，x∈（0，1）時，函數y=h（x）的圖象總在直線y=1-x的上方，求P的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•吉安縣模擬）已知函數y=f（x）對任意的實數x，y都有f（x+y）=f（x）•f（y）且f（1）≠0
（1）記an=f(n)，(n∈N*)，Sn=
n
i=1
ai，設bn=
2Sn
an
+1且{bn}為等比數列，求a1的值；
（2）在（1）的條件下，設Cn=
1
1+2an
證明：
（i）對任意的x＞0，Cn≥
1
1+x
-
1
(1+x)2
(2an-x)n∈N*
（ii） C1+C2+…+Cn＞
n2
n+1
n∈N*．

查看答案和解析>>

科目：高中數學 來源： 題型：

給出下列五個命題：其中正確的命題有
②③④
②③④
（填序號）．
①函數y=sinx（x∈[-π，π]）的圖象與x軸圍成的圖形的面積S=
∫
π
-π
sinxdx；
②
C
r+1
n+1
=
C
r+1
n
+
C
r
n
；
③在（a+b）n的展開式中，奇數項的二項式系數之和等于偶數項的二項式系數之和；
④i+i2+i3+…i2012=0；
⑤用數學歸納法證明不等式
1
n+1
+
1
n+2
+
1
n+3
+…+
1
2n
＞
13
24
，(n≥2，n∈N*)的過程中，由假設n=k成立推到n=k+1成立時，只需證明
1
k+1
+
1
k+2
+
1
k+3
+…+
1
2k
+
1
2k+1
+
1
2(k+1)
＞
13
24
即可．

查看答案和解析>>

同步練習冊答案