
((本小題14分)
已知函數(shù)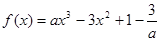
(I)若函數(shù)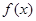 在
在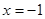 時(shí)取得極值,求實(shí)數(shù)
時(shí)取得極值,求實(shí)數(shù)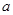 的值;
的值;
(II)試討論函數(shù)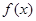 的單調(diào)性;
的單調(diào)性;

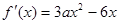 (
(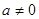 )
……………………………1分
)
……………………………1分
(I)∵函數(shù)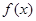 在
在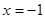 時(shí)取到極值
時(shí)取到極值
∴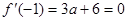 解得
解得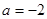
經(jīng)檢驗(yàn)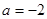 函數(shù)
函數(shù)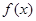 在
在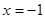 時(shí)取到極小值(不檢驗(yàn)扣1分)
時(shí)取到極小值(不檢驗(yàn)扣1分)
∴實(shí)數(shù)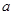 的值-2
…………………………4分
的值-2
…………………………4分
(II)由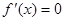 得
得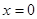 或
或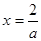 …………………………5分
…………………………5分
①當(dāng)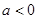 時(shí),
時(shí),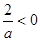
由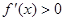 得
得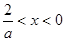
由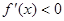 得
得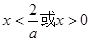
∴函數(shù)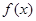 得單調(diào)增區(qū)間為
得單調(diào)增區(qū)間為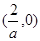 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為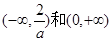 …………7分
…………7分
②當(dāng)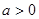 時(shí),
時(shí), ,同理可得函數(shù)
,同理可得函數(shù)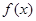 得單調(diào)增區(qū)間為
得單調(diào)增區(qū)間為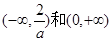 ,
,
單調(diào)減區(qū)間為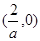 ………………………………9分
………………………………9分
(II)假設(shè)存在滿足要求的兩點(diǎn)A,B,即在點(diǎn)A、B處的切線都與y軸垂直,則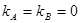
即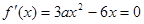 解得
解得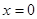 或
或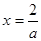
∴A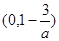 ,B
,B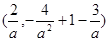

【解析】略


 計(jì)算高手系列答案
計(jì)算高手系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(本小題14分)記函數(shù)![]() 的定義域?yàn)?IMG src='http://thumb.zyjl.cn/pic1/img/20091015/20091015203835002.gif' width=16 height=17>,
的定義域?yàn)?IMG src='http://thumb.zyjl.cn/pic1/img/20091015/20091015203835002.gif' width=16 height=17>,
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (本小題14分)右圖是一個(gè)直三棱柱(以
(本小題14分)右圖是一個(gè)直三棱柱(以![]() 為底面)
為底面)
被一平面所截得到的幾何體,截面為ABC.
已知![]() .
.
(1)設(shè)點(diǎn)O是AB的中點(diǎn),證明:OC∥平面A1B1C1;
(2)證明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此幾何體的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題14分)已知![]()
(1)若![]() 求
求![]() 的表達(dá)式.
的表達(dá)式.
(2)若函數(shù)![]() 和函數(shù)
和函數(shù)![]() 的圖象關(guān)于原點(diǎn)對稱,求
的圖象關(guān)于原點(diǎn)對稱,求![]() 的解析式.
的解析式.
(3)若![]() 在
在![]() 上是增函數(shù),求實(shí)數(shù)l的取值范圍.
上是增函數(shù),求實(shí)數(shù)l的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣東省肇慶市高三復(fù)習(xí)必修五綜合練習(xí) 題型:解答題
(本小題14分)如圖所示,L是海面上一條南北方向的海防警戒線,在L上點(diǎn)A處有一個(gè)水聲監(jiān)測點(diǎn),另兩個(gè)監(jiān)測點(diǎn)B,C分別在A的正東方20 km處和54 km處.某時(shí)刻,監(jiān)測點(diǎn)B收到發(fā)自靜止目標(biāo)P的一個(gè)聲波,8s后監(jiān)測點(diǎn)A,20 s后監(jiān)測點(diǎn)C相繼收到這一信號.在當(dāng)時(shí)氣象條件下,聲波在水中的傳播速度是1. 5 km/s.
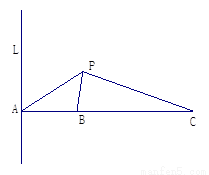
(1)設(shè)A到P的距離為 km,用
km,用 分別表示B、C到P 的距離,并求
分別表示B、C到P 的距離,并求 值;
值;
(2)求靜止目標(biāo)P到海防警戒線L的距離(結(jié)果精確到0.01 km)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣東省肇慶市高三復(fù)習(xí)必修五綜合練習(xí) 題型:解答題
(本小題14分)在等差數(shù)列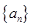 中,
中,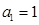 ,前
,前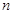 項(xiàng)和
項(xiàng)和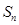 滿足條件
滿足條件 ,
,
(1)求數(shù)列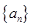 的通項(xiàng)公式和
的通項(xiàng)公式和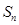 ;
;
(2)記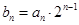 ,求數(shù)列
,求數(shù)列 的前
的前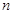 項(xiàng)和
項(xiàng)和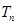
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com