中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

為調查某社區居民的業余生活狀況，研究這一社區居民在20：00－22：00時間段的休閑方式與性別的關系，隨機調查了該社區80人，得到下面的數據表：

     休閑方式
性別  
看電視
看書
合計
男
10
50
60
女
10
10
20
合計
20
60
80
 
(1)將此樣本的頻率估計為總體的概率，隨機調查3名在該社區的男性，設調查的3人在這一時間段以看書為休閑方式的人數為隨機變量X，求X的分布列和數學期望；
(2)根據以上數據，我們能否在犯錯誤的概率不超過0．01的前提下，認為“在20：00－22：00時間段居民的休閑方式與性別有關系”？
參考公式：K2＝，其中n＝a＋b＋c＋d．
參考數據：
P(K2≥k0)
0．15
0．10
0．05
0．025
0．010
k0
2．072
2．706
3．841
5．024
6．635
 

（1）P(X＝k)＝()3－k()k，k＝0,1,2,3．
E(X)＝np＝3×＝．
（2）休閑方式與性別無關系

解析

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

某高校共有15000人，其中男生10500人，女生4500人，為調查該校學生每周平均體育運動時間的情況，采用分層抽樣的方法，收集300位學生每周平均體育運動時間的樣本數據（單位:小時）
（1）應收集多少位女生樣本數據？
（2）根據這300個樣本數據，得到學生每周平均體育運動時間的頻率分布直方圖（如圖所示），其中樣本數據分組區間為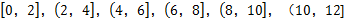：.估計該校學生每周平均體育運動時間超過4個小時的概率.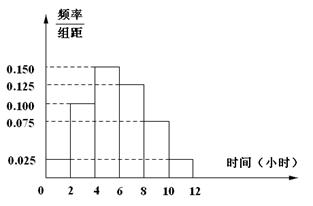

（3）在樣本數據中，有60位女生的每周平均體育運動時間超過4個小時.請完成每周平均體育運動時間與性別的列聯表，并判斷是否有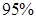的把握認為“該校學生的每周平均體育運動時間與性別有關”.
附：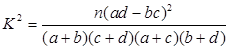


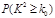0.10
0.05
0.010
0.005

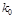2.706
3.841
6.635
7.879
 

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（2013•天津）一個盒子里裝有7張卡片，其中有紅色卡片4張，編號分別為1，2，3，4； 白色卡片3張，編號分別為2，3，4．從盒子中任取4張卡片 （假設取到任何一張卡片的可能性相同）．
（1）求取出的4張卡片中，含有編號為3的卡片的概率．
（2）再取出的4張卡片中，紅色卡片編號的最大值設為X，求隨機變量X的分布列和數學期望．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某中學將100名高一新生分成水平相同的甲、乙兩個“平行班”，每班50人．陳老師采用A、B兩種不同的教學方式分別在甲、乙兩個班級進行教改實驗．為了了解教學效果，期末考試后，陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計，作出莖葉圖如下．記成績不低于90分者為“成績優秀”．

甲
 
乙
6
9
3 6 7 9 9
9 5 1 0
8
0 1 5 6
9 9 4 4 2
7
3 4 5 8 8 8
8 8 5 1 1 0
6
0 7 7
4 3 3 2
5
2 5
 
(1)在乙班樣本中的20個個體中，從不低于86分的成績中隨機抽取2個，求抽出的兩個均“成績優秀”的概率；
(2)由以上統計數據填寫下面列聯表，并判斷是否有90%的把握認為：“成績優秀”與教學方式有關.
 
甲班(A方式)
乙班(B方式)
總計
成績優秀
 
 
 
成績不優秀
 
 
 
總計
 
 
 
 
附：,其中n＝a＋b＋c＋d.)
 P(K2≥k)
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
   k
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
 

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某商店試銷某種商品20天，獲得如下數據：

日銷售量（件）
0
1
2
3
頻數
1
5
9
5
 
試銷結束后（假設該商品的日銷售量的分布規律不變），設某天開始營業時有該商品3件，當天營業結束后檢查存貨，若發現存貨少于2件，則當天進貨補充至3件，否則不進貨，將頻率視為概率。
（1）求當天商品不進貨的概率；
（2）記X為第二天開始營業時該商品的件數，求X的分布列和數學期望。

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

甲、乙兩人各擲一次骰子（均勻的正方體，六個面上分別為1,2,3,4,5,6點），所得點數分別為x,y
(1)求x<y的概率；
（2）求5<x+y<10的概率。

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

甲、乙兩射手在同一條件下進行射擊，分布列如下：射手甲擊中環數8，9，10的概率分別為0.2，0.6，0.2；射手乙擊中環數8，9，10的概率分別為0.4，0.2，0.4.用擊中環數的期望與方差比較兩名射手的射擊水平．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

甲向靶子A射擊兩次，乙向靶子射擊一次.甲每次射擊命中靶子的概率為0.8，命中得5分；乙命中靶子的概率為0.5，命中得10分.
（1）求甲、乙二人共命中一次目標的概率；
（2）設X為二人得分之和，求X的分布列和期望.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（2011•山東）甲、乙兩校各有3名教師報名支教，期中甲校2男1女，乙校1男2女．
（1）若從甲校和乙校報名的教師中各任選1名，寫出所有可能的結果，并求選出的2名教師性別相同的概率；
（2）若從報名的6名教師中任選2名，寫出所有可能的結果，并求選出的2名教師來自同一學校的概率．

查看答案和解析>>

同步練習冊答案