
有4個不同的球,四個不同的盒子,把球全部放入盒內.
(1)共有多少種放法?
(2)恰有一個盒子不放球,有多少種放法?
(3)恰有一個盒內放2個球,有多少種放法?
(4)恰有兩個盒不放球,有多少種放法?
(1)256(2)144(3)144(4)84
解析試題分析:(1)一個球一個球地放到盒子里去,每只球都可有4種獨立的放法,由分步乘法計數原理,放法共有: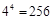 種.
種.
(2)為保證“恰有一個盒子不放球”,先從四個盒子中任意拿出去1個,即將4個球分成2,1,1的三組,有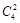 種分法;然后再從三個盒子中選一個放兩個球,其余兩個球,兩個盒子,全排列即可.由分步乘法計數原理,共有放法:
種分法;然后再從三個盒子中選一個放兩個球,其余兩個球,兩個盒子,全排列即可.由分步乘法計數原理,共有放法: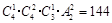 種.
種.
(3)“恰有一個盒內放2個球”,即另外三個盒子中恰有一個空盒.因此,“恰有一個盒內放2球”與“恰有一個盒子不放球”是一回事.故也有144種放法.
(4)先從四個盒子中任意拿走兩個有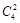 種,問題轉化為:“4個球,兩個盒子,每盒必放球,有幾種放法?”從放球數目看,可分為(3,1),(2,2)兩類.第一類:可從4個球中先選3個,然后放入指定的一個盒子中即可,有
種,問題轉化為:“4個球,兩個盒子,每盒必放球,有幾種放法?”從放球數目看,可分為(3,1),(2,2)兩類.第一類:可從4個球中先選3個,然后放入指定的一個盒子中即可,有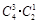 種放法;第二類:有
種放法;第二類:有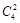 種放法.因此共有
種放法.因此共有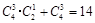 種.由分步乘法計數原理得“恰有兩個盒子不放球”的放法有:
種.由分步乘法計數原理得“恰有兩個盒子不放球”的放法有: 種.
種.
考點:本小題主要考查兩個計數原理和排列組合的綜合應用.
點評:兩個計數原理是解決這類問題的基礎,而排列組合的準確靈活應用是解決這類問題的關鍵,要分清是排列問題還是組合問題,是分類還是分步,要堅持特殊元素優先和特殊位置優先的原則.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某班同學利用寒假在5個居民小區內選擇兩個小區逐戶進行一次“低碳生活習慣”的調查,以計算每戶的碳月排放量.若月排放量符合低碳標準的稱為“低碳族”,否則稱為“非低碳族”.若小區內有至少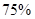 的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區” .已知備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區” .已知備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
(Ⅰ)求所選的兩個小區恰有一個為“非低碳小區”的概率;
(Ⅱ)假定選擇的“非低碳小區”為小區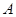 ,調查顯示其“低碳族”的比例為
,調查顯示其“低碳族”的比例為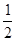 ,數據如圖1所示,經過同學們的大力宣傳,三個月后,又進行了一次調查,數據如圖2所示,問這時小區
,數據如圖1所示,經過同學們的大力宣傳,三個月后,又進行了一次調查,數據如圖2所示,問這時小區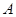 是否達到“低碳小區”的標準?
是否達到“低碳小區”的標準?
|
|

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有5個男生和3個女生,從中選取5人擔任5門不同學科的科代表,求分別符合下列條件的選法數:
(1)有女生但人數必須少于男生.
(2)某女生一定要擔任語文科代表.
(3)某男生必須包括在內,但不擔任數學科代表.
(4)某女生一定要擔任語文科代表,某男生必須擔任科代表,但不擔任數學科代表.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1)用1、2、3、4、5、6、7可組成多少個無重復數字的四位數且四位數為偶數;
(2)用0、1、2、3、4、5可組成多少無重復數字的且可被5整除的五位數. (用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有6本不同的書,按照以下要求處理,各有多少種不同的分法?
(1)一堆一本,一堆兩本,一堆三本;
(2)甲得一本,乙得兩本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分給甲、乙、丙三人;
(5)平均分成三堆.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有4名男生、5名女生,全體排成一行,問下列情形各有多少種不同的排法?
(1)甲不在中間也不在兩端;
(2)甲、乙兩人必須排在兩端;
(3)男、女生分別排在一起;
(4)男女相間;
(5)甲、乙、丙三人從左到右順序保持一定.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com