
(本題12分)已知等比數列{an}的公比q=3,前3項和S3=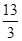 .
.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)若函數f(x)=Asin(2x+φ)(A>0,0<φ<π)在x=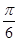 處取得最大值,且最大值為a3,
處取得最大值,且最大值為a3,
求函數f(x)的解析式.
(1)an= ×3n-1=3n-2.(2)f(x)=3sin
×3n-1=3n-2.(2)f(x)=3sin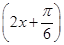 .
.
【解析】本試題主要是結合數列的概念得到數列的通項公式,然后結合三角函數中的性質得最值問題,從而求解得到解析式。
(1)利用等比數列{an}的公比q=3,前3項和S3=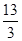 ,結合前n項和公式解得首項,從而得到通項公式
,結合前n項和公式解得首項,從而得到通項公式
(2)中利用第一問的結論,得到a3=3,從而得到函數的振幅,同時把x=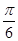 代入解析式中,是的函數取得最大值,得到φ的值,從而求解得到解析式。
代入解析式中,是的函數取得最大值,得到φ的值,從而求解得到解析式。
解:(Ⅰ)由q=3,S3=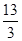 得
得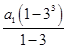 =
=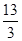 ,解得a1=
,解得a1= . 所以an=
. 所以an= ×3n-1=3n-2.
×3n-1=3n-2.
(Ⅱ)由(1)可知an=3n-2,所以a3=3. 因為函數f(x)的最大值為3,所以A=3;因為當x=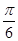 時f(x)取得最大值,所以sin
時f(x)取得最大值,所以sin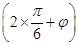 =1. 又0<φ<π,故φ=
=1. 又0<φ<π,故φ=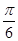 .
.
所以函數f(x)的解析式為f(x)=3sin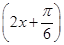 .
.


科目:高中數學 來源:2011屆山東省濟寧市一中高三第一次調研考試數學理卷 題型:解答題
(本題滿分12分)
已知 成等差數列.又數列
成等差數列.又數列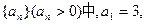 此數列的前n項的和Sn(
此數列的前n項的和Sn(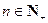 )對所有大于1的正整數n都有
)對所有大于1的正整數n都有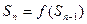 .
.
(1)求數列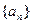 的第n+1項;
的第n+1項;
(2)若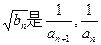 的等比中項,且Tn為{bn}的前n項和,求Tn.
的等比中項,且Tn為{bn}的前n項和,求Tn.
查看答案和解析>>
科目:高中數學 來源:2011屆本溪縣高二暑期補課階段考試數學卷 題型:解答題
(本題滿分12分)已知各項均為正數的數列 ,
, 的等比中項。
的等比中項。
(1)求證:數列 是等差數列;(2)若
是等差數列;(2)若 的前n項和為Tn,求Tn。
的前n項和為Tn,求Tn。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年本溪縣高二暑期補課階段考試數學卷 題型:解答題
(本題滿分12分)已知各項均為正數的數列 ,
,
 的等比中項。
的等比中項。
(1)求證:數列 是等差數列;(2)若
是等差數列;(2)若 的前n項和為Tn,求Tn。
的前n項和為Tn,求Tn。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年山東省濟寧市高三第一次調研考試數學理卷 題型:解答題
(本題滿分12分 )
已知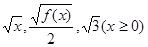 成等差數列.又數列
成等差數列.又數列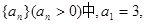 此數列的前n項的和Sn(
此數列的前n項的和Sn(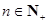 )對所有大于1的正整數n都有
)對所有大于1的正整數n都有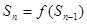 .
.
(1)求數列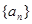 的第n+1項;
的第n+1項;
(2)若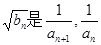 的等比中項,且Tn為{bn}的前n項和,求Tn.
的等比中項,且Tn為{bn}的前n項和,求Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分 )
已知![]() 成等差數列.又數列
成等差數列.又數列![]() 此數列的前n項的和Sn(
此數列的前n項的和Sn(![]() )對所有大于1的正整數n都有
)對所有大于1的正整數n都有![]() .
.
(1)求數列![]() 的第n+1項;
的第n+1項;
(2)若![]() 的等比中項,且Tn為{bn}的前n項和,求Tn.
的等比中項,且Tn為{bn}的前n項和,求Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com