
 ,證明:
,證明: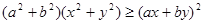 ,并利用上述結論求
,并利用上述結論求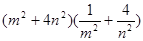 的最小值(其中
的最小值(其中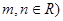 .
.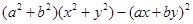 作差后關鍵就是變形確定符號,將其展開 后合并同類項得
作差后關鍵就是變形確定符號,將其展開 后合并同類項得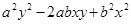 ,這個式子剛好就是一個完全平方
,這個式子剛好就是一個完全平方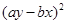 ,而
,而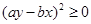 ,所以有
,所以有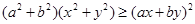 。也可以用分析法等來證明。分析法是從求證的不等式出發,分析使這個不等式成立的充分條件,把證明不等式轉化為判定這些充分條件是否具備的問題。如果能夠肯定這些充分條件都已具備,那么就可以斷定原不等式成立,這種證明方法叫做分析法。如本題中要證明
。也可以用分析法等來證明。分析法是從求證的不等式出發,分析使這個不等式成立的充分條件,把證明不等式轉化為判定這些充分條件是否具備的問題。如果能夠肯定這些充分條件都已具備,那么就可以斷定原不等式成立,這種證明方法叫做分析法。如本題中要證明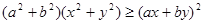 ,則找使得這個不等式成立的充分條件
,則找使得這個不等式成立的充分條件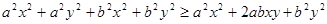 依次找下去,最后得到
依次找下去,最后得到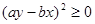 (顯然成立),所以不等式得證。
(顯然成立),所以不等式得證。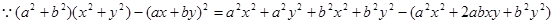
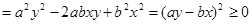 4分
4分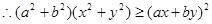 7分
7分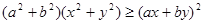
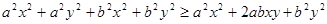 2分
2分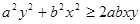 4分
4分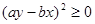 (顯然成立)
(顯然成立)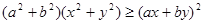 成立
成立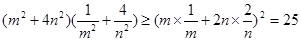 , 10分
, 10分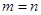 時等號成立。 13分
時等號成立。 13分

 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數學 來源:不詳 題型:解答題
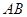 、
、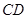 與橋面
與橋面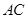 垂直,通過測量得知
垂直,通過測量得知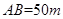 ,
,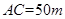 ,當
,當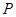 為
為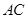 中點時,
中點時,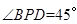 .
.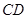 的長;
的長;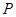 在線段
在線段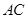 的何處時,
的何處時,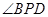 達到最大.
達到最大.
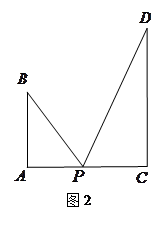
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com