
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
A
解法一:由已知得f-1(x)=loga(x+![]() )>1=logaa,
)>1=logaa,
∴x+![]() >a,∴
>a,∴![]() >a-x.
>a-x.
又![]() >a-x
>a-x![]() a-x≤0或
a-x≤0或![]()
![]() x≥a或
x≥a或![]() <x<a
<x<a![]() x>
x>![]() ,故選A.
,故選A.
解法二:f(x)=![]() (ax-a-x)(a>1),
(ax-a-x)(a>1),
當a>1時,y=ax單增;當a>1時,y=a-x單減.
∴f(x)=![]() (ax-a-x)單增.∴f-1(x)也單增.
(ax-a-x)單增.∴f-1(x)也單增.
f-1(x)>1說明反函數的值域是(1,+∞),即原函數f(x)的定義域是(1,+∞).
求f-1(x)>1中x的取值范圍,即求反函數的x的取值范圍,只要求原函數f(x)在(1,+∞)上的值域.
又f(x)單增,∴f(x)>f(1),即f(x)>![]() .
.
∴f-1(x)>1中的x>![]() .故選A.
.故選A.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2010-2011學年四川省南充市高三第二次診斷性考試理科數學卷 題型:選擇題
設 是函數
是函數 的反函數,則使
的反函數,則使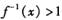 成立的x的取值范圍是( )
成立的x的取值范圍是( )
A.( ,
, ) B.
(
) B.
( ,
, ) C.
(O,
) C.
(O, ) D.
(
) D.
( ,0)
,0)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com