A、解:(1)∵f(x)為奇函數,
故f(x)的定義域關于原點對稱
又f(x)的定義域為
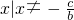
(顯然b≠0,否則f(x)為偶函數)
∴
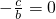
,即c=0
于是得

,且

,

∴

∴
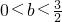
,又b∈Z
∴b=1
∴a=1
故a=b=1,c=0,符合f(x)在[1,+∞)上單調遞增
(2)由(1)知

,
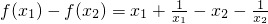
=

①當-1<x
1<x
2<0時,顯然x
1-x
2<0,0<x
1x
2<1,x
1x
2-1<0
∴f(x
1)-f(x
2)>0
∴f(x)為減函數
②當x
1<x
2<-1時,顯然x
1-x
2<0,x
1x
2>1,x
1x
2-1>0
∴f(x
1)-f(x
2)<0
∴f(x)為增函數
綜上所述,f(x)在(-∞,-1]上是增函數,在[-1,0)上是減函數.
B、解:由題意二次函數f(x)圖象開口向下,
故在對稱軸兩邊的圖象是左降右升
又對于任意實數x,都有f(2-x)=f(x+2),
故此函數的對稱軸方程是x=2
由此知,函數f(x)在(-∞,2]上是增函數,在(2,+∞)是減函數,
而x
2+x+

=(x+

)
2+

≥

,2x
2-x+

=2(x-

)
2+

≥

,
∴

(x
2+x+

)≤

=2,

(2x
2-x+

)≤

=1,
∵f[

(x
2+x+

)]<f[

(2x
2-x+

)]
∴

(x
2+x+

)<

(2x
2-x+

),
∴x
2+x+

>2x
2-x+

,解得

,
∴不等式的解集為

.
分析:A、(1)求三個未知數,需要三個條件,一是定義域要關于原點對稱,二是f(1)=2,三是f(2)<3,f(x)在[1,+∞)上單調遞增可解.
(2)用單調性定義來探討,先在給定的區間上任取兩個變量,且界定大小,再作差變形,在與0比較中出現討論,再進一步細化區間,確定后即為所求的單調區間.
B、由題設二次函數f(x)的圖象開口向下,又對于任意實數x,都有f(2-x)=f(x+2),知其對稱軸方程為x=2,由二次函數的這些特征即可研究出其單調性,分析

(x
2+x+

),

(2x
2-x+

)的范圍,利用二次函數的單調性轉化不等式為

(x
2+x+

)<

(2x
2-x+

),利用對數函數的單調性把不等式轉化為x
2+x+

>2x
2-x+

,解此不等式即可求得結果.
點評:A、此題是中檔題.本題主要考查函數利用奇偶性和函數值,單間性來求解析式,在研究單調性中分類討論的思想應用.
B、本題主要考查二次函數的單調性和對稱性,還考查了利用對數函數的單調性解對數不等式和一元二次不等式的解法,特別注意對數不等式的求解時的定義域.

 是奇函數,又f(1)=2,f(2)<3,且f(x)在[1,+∞)上遞增.
是奇函數,又f(1)=2,f(2)<3,且f(x)在[1,+∞)上遞增. (x2+x+
(x2+x+ )]<f[
)]<f[ (2x2-x+
(2x2-x+ )]的解.
)]的解.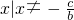 (顯然b≠0,否則f(x)為偶函數)
(顯然b≠0,否則f(x)為偶函數)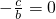 ,即c=0
,即c=0 ,且
,且  ,
,

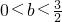 ,又b∈Z
,又b∈Z ,
,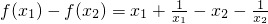 =
=
 =(x+
=(x+ )2+
)2+ ≥
≥ ,2x2-x+
,2x2-x+ =2(x-
=2(x- )2+
)2+ ≥
≥ ,
, (x2+x+
(x2+x+ )≤
)≤ =2,
=2, (2x2-x+
(2x2-x+ )≤
)≤ =1,
=1, (x2+x+
(x2+x+ )]<f[
)]<f[ (2x2-x+
(2x2-x+ )]
)] (x2+x+
(x2+x+ )<
)< (2x2-x+
(2x2-x+ ),
), >2x2-x+
>2x2-x+ ,解得
,解得 ,
, .
. (x2+x+
(x2+x+ ),
), (2x2-x+
(2x2-x+ )的范圍,利用二次函數的單調性轉化不等式為
)的范圍,利用二次函數的單調性轉化不等式為 (x2+x+
(x2+x+ )<
)< (2x2-x+
(2x2-x+ ),利用對數函數的單調性把不等式轉化為x2+x+
),利用對數函數的單調性把不等式轉化為x2+x+ >2x2-x+
>2x2-x+ ,解此不等式即可求得結果.
,解此不等式即可求得結果.

 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案