
已知函數(shù)f(x)=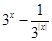 .
.
(1)若f(x)=2,求x的值;
(2)判斷x>0時,f(x)的單調性;
(3)若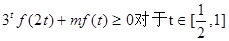 恒成立,求m的取值范圍。
恒成立,求m的取值范圍。
(1) x=log3(1+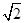 ) ;
) ;
(2) f(x)=3x-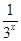 在(0,+∞)上單調遞增 ;
在(0,+∞)上單調遞增 ;
(3) [-4,+∞).
【解析】
試題分析:(1)當x≤0時,f(x)=3x-3x=0,∴f(x)=2無解.
當x>0時,f(x)=3x-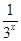 ,令3x-
,令3x-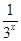 =2,
=2,
∴(3x)2-2·3x-1=0,∴3x=1±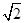 .
.
∵3x>0,∴3x=1-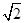 (舍).∴3x=1+
(舍).∴3x=1+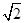 .∴x=log3(1+
.∴x=log3(1+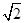 )
4分
)
4分
(2)當x>0,f(x)=3x-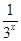 .∵y=3x在(0,+∞)上單調遞增,
.∵y=3x在(0,+∞)上單調遞增,
y=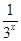 在(0,+∞)上單調遞減.
在(0,+∞)上單調遞減.
∴f(x)=3x-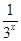 在(0,+∞)上單調遞增
8分
在(0,+∞)上單調遞增
8分
(3)∵t∈[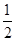 ,1],∴f(t)=3t-
,1],∴f(t)=3t-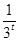 >0,
>0,
∴3tf(2t)+mf(t)≥0化為3t(32t-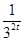 )+m(3t-
)+m(3t-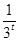 )≥0.
)≥0.
即3t(3t+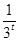 )+m≥0.即m≥-32t-1.
)+m≥0.即m≥-32t-1.
令g(t)=-32t-1,則g(t)在[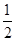 ,1]上遞減,
,1]上遞減,
∴g(x)max=-4.
∴所求實數(shù)m的取值范圍是[-4,+∞) 13分
考點:本題主要考查指數(shù)函數(shù)的性質,指數(shù)方程的解法,不等式恒成立問題。
點評:中檔題,解簡單的指數(shù)方程,一般是考慮化同底數(shù)指數(shù)冪相等或利用“換元法”,轉化成一元二次方程求解。不等式恒成立問題,一般是利用“分離參數(shù)法”,轉化成求函數(shù)最值問題。


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數(shù)學 來源: 題型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 已知函數(shù)f(x)=
已知函數(shù)f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 2x-2-x | 2x+2-x |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| x-1 | x+a |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com