已知命題p:?x∈R,使得k+|x-2|≥|x-1|;命題q:?x,y∈R+且x+y=1,有xyk≤x+4y.若p∧q為真,則實數k的取值范圍是( )
A.[-1,9]
B.[1,9]
C.[-1,8]
D.[1,8]
【答案】
分析:本題考查復合命題,解決的方法是:將k+|x-2|≥|x-1|和xyk≤x+4y分別變形后求出k的取值范圍,最后求交集.
解答:解:命題p:?x∈R,使得k+|x-2|≥|x-1|成立,
∴有:?x∈R,k≥|x-1|-|x-2|成立,
∴只須:k大于等于(|x-1|-|x-2|)的最小值即可,
而由絕對值的幾何意義可知|x-1|-|x-2|表示數軸上的點到1和2的距離之差,

由上圖分析得:當實數x在數軸上移動時有:-1≤|x-1|-|x-2|≤1,
即:k≥-1.
命題q:?x,y∈R
+且x+y=1,有xyk≤x+4y,
∴有:
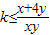
對?x,y∈R
+且滿足x+y=1的實數x、y成立,
∴只須:k小于等于
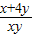
的最小值即可,
而

=

=

=5+
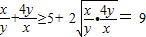
,
即:k≤9.
又∵p∧q為真,
∴命題p和命題q均為真命題,
∴應有
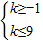
,解得:-1≤k≤9,即:[-1,9].
故選A.
點評:本題以復合命題的真假為載體,主要考查絕對值的幾何意義及不等式求函數的最值的掌握情況,要做到熟練掌握.


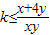 對?x,y∈R+且滿足x+y=1的實數x、y成立,
對?x,y∈R+且滿足x+y=1的實數x、y成立,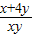 的最小值即可,
的最小值即可, =
= =
= =5+
=5+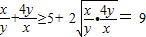 ,
,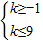 ,解得:-1≤k≤9,即:[-1,9].
,解得:-1≤k≤9,即:[-1,9].
