
下圖是某游戲中使用的材質均勻的圓形轉盤,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面積各占轉盤面積的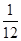 ,
,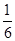 ,
,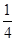 ,
,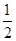 .游戲規則如下:
.游戲規則如下: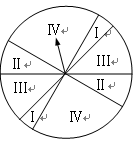
① 當指針指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分時,分別獲得積分100分,40分,10分,0分;
② (ⅰ)若參加該游戲轉一次轉盤獲得的積分不是40分,則按①獲得相應的積分,游戲結束;
(ⅱ)若參加該游戲轉一次獲得的積分是40分,則用拋一枚質地均勻的硬幣的方法來決定是否繼續游戲.正面向上時,游戲結束;反面向上時,再轉一次轉盤,若再轉一次的積分不高于40分,則最終積分為0分,否則最終積分為100分,游戲結束.
設某人參加該游戲一次所獲積分為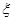 .
.
(1)求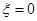 的概率;
的概率;
(2)求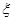 的概率分布及數學期望.
的概率分布及數學期望.
科目:高中數學 來源: 題型:解答題
一個盒子中裝有4張卡片,每張卡片上寫有1個數字,數字分別是1、2、3、4,現從盒子中隨機抽取卡片.
(Ⅰ)若一次從中隨機抽取3張卡片,求3張卡片上數字之和大于或等于7的概率;
(Ⅱ)若第一次隨機抽取1張卡片,放回后再隨機抽取1張卡片,求兩次抽取的卡片中至少一次抽到數字2的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩個盒子中各有3個球,其中甲盒中有2個黑球1個白球,乙盒中有1個黑球2個白球,所有球之間只有顏色區別.
(Ⅰ)若從甲、乙兩個盒子中各取一個球,求取出的2個球顏色相同的概率;
(Ⅱ)將這兩個盒子中的球混合在一起,從中任取2個, 求取出的2個球中至少有一個黑球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲乙兩隊參加知識競賽,每隊 人,每人回答一個問題,答對者為本隊贏得一分,答錯得零分。假設甲隊中每人答對的概率均為
人,每人回答一個問題,答對者為本隊贏得一分,答錯得零分。假設甲隊中每人答對的概率均為 ,乙隊中
,乙隊中 人答對的概率分別為
人答對的概率分別為 且各人正確與否相互之間沒有影響.用
且各人正確與否相互之間沒有影響.用 表示甲隊的總得分.
表示甲隊的總得分.
(Ⅰ)求隨機變量 分布列
分布列
(Ⅱ)用 表示“甲、乙兩個隊總得分之和等于
表示“甲、乙兩個隊總得分之和等于 ”這一事件,用
”這一事件,用 表示“甲隊總得分大于乙隊總得分”這一事件,求
表示“甲隊總得分大于乙隊總得分”這一事件,求 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某普通高中共有教師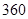 人,分為三個批次參加研修培訓,在三個批次中男、女教師人數如下表所示:
人,分為三個批次參加研修培訓,在三個批次中男、女教師人數如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教師 | 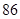 | 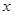 | 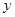 |
| 男教師 | 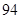 |  | 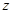 |
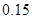 、
、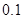 .
.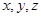 的值;
的值;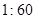 的比例抽取教師進行問卷調查,三個批次被選取的人數分別是多少?
的比例抽取教師進行問卷調查,三個批次被選取的人數分別是多少?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在進行一項擲骰子放球的游戲中規定:若擲出1點或2點,則在甲盒中放一球;否則,在乙盒中放一球。現在前后一共擲了4次骰子,設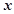 、
、 分別表示甲、乙盒子中球的個數。
分別表示甲、乙盒子中球的個數。
(Ⅰ)求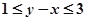 的概率;
的概率;
(Ⅱ)若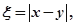 求隨機變量
求隨機變量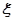 的分布列和數學期望。
的分布列和數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲乙兩班進行消防安全知識競賽,每班出3人組成甲乙兩支代表隊,首輪比賽每人一道必答題,答對則為本隊得1分,答錯不答都得0分,已知甲隊3人每人答對的概率分別為 ,乙隊每人答對的概率都是
,乙隊每人答對的概率都是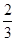 .設每人回答正確與否相互之間沒有影響,用
.設每人回答正確與否相互之間沒有影響,用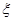 表示甲隊總得分.
表示甲隊總得分.
(I)求隨機變量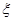 的分布列及其數學期望E(
的分布列及其數學期望E(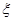 );
);
(Ⅱ)求在甲隊和乙隊得分之和為4的條件下,甲隊比乙隊得分高的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
現有6道題,其中4道甲類題,2道乙類題,張同學從中任取3道題解答.試求
(I)所取的2道題都是甲類題的概率;
(II)所取的2道題不是同一類題的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com