
�ԙE�A ��һ����c(di��n)
��һ����c(di��n) ��ֱ����c(di��n)���˙E�A�ă�(n��i)�ӵ���ֱ��������
��ֱ����c(di��n)���˙E�A�ă�(n��i)�ӵ���ֱ�������� ��ԇ������1���@�ӵĵ���ֱ���������Ƿ���ڣ������ڣ�����һ������ֱ�������������ڵ�ֱ�����̡��������ڣ��f�����ɡ���2���@�ӵĵ���ֱ�������������ڣ�����Ўׂ���
��ԇ������1���@�ӵĵ���ֱ���������Ƿ���ڣ������ڣ�����һ������ֱ�������������ڵ�ֱ�����̡��������ڣ��f�����ɡ���2���@�ӵĵ���ֱ�������������ڣ�����Ўׂ���
(1)���ڣ�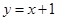 �c
�c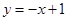 ����2�����ڣ������
����2�����ڣ������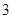 ��.
��.
����ԇ�}��������1���@�ӵĵ���ֱ�������δ��ڣ�ֱ��y=x+1�cֱ��y=-x+1�M���}�⣻
��2���O(sh��)��CA���ڵ�ֱ�����̣�����E�A�ķ��̲����������|CA|��ͬ�����|CB|����|CA|=|CB|�ã�k-1��[k2-��a2-1��k+1]=0��ӑՓ���̸�����r�����ɵó��Y(ji��)Փ��
ԇ�}��������1���@�ӵĵ���ֱ�������δ��ڡ���?y��n)�ֱ��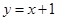 �cֱ��
�cֱ��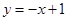 ��ֱ�����P(gu��n)��
��ֱ�����P(gu��n)�� �S���Q������ֱ��
�S���Q������ֱ��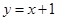 �cֱ��
�cֱ��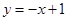 ��һ������ֱ�������������ڵ�ֱ�����̡�
��һ������ֱ�������������ڵ�ֱ�����̡�
��2���O(sh��)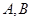 ���c(di��n)�քe����
���c(di��n)�քe���� �S�����҃ɂ�(c��)���O(sh��)
�S�����҃ɂ�(c��)���O(sh��)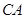 ��б�ʞ�
��б�ʞ� ���t
���t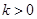 ��
��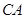 ���ڵ�ֱ�����̞�
���ڵ�ֱ�����̞�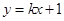 ������E�A�ķ��̲�������
������E�A�ķ��̲�������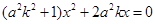 ��
��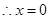 ��
��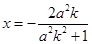 ��
��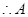 �ęM����(bi��o)��
�ęM����(bi��o)��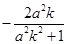 ��
��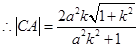 ��
��
ͬ���ɵ� ��������
��������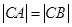 ��
��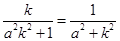 ��
��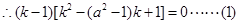 ��
��
��(d��ng)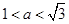 �r����1���Ľ���
�r����1���Ľ���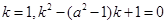 �o��(sh��)��(sh��)�⣻
�o��(sh��)��(sh��)�⣻
��(d��ng)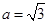 �r����1���Ľ���
�r����1���Ľ���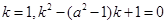 �Ľ�Ҳ��
�Ľ�Ҳ��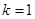 ����(d��ng)
����(d��ng)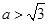 �r����1���Ľ��
�r����1���Ľ��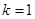 �⣬����
�⣬����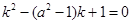 �Ѓɂ�����ȵ��������Ҷ������ڣ��ʣ�1����
�Ѓɂ�����ȵ��������Ҷ������ڣ��ʣ�1���� 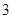 ��������
��������
���Է����}��ĵ���ֱ��������һ�����ڣ������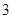 ����
����
���c(di��n)��(1)�E�A�����|(zh��)����2��ֱ���c�A�F�����đ�(y��ng)��.


 ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵxOy��,��֪�AP��x�S�Ͻصþ����L��2 ,��y�S�Ͻصþ����L��2
,��y�S�Ͻصþ����L��2 .
.
(1)��A��P��܉�E����;
(2)��P�c(di��n)��ֱ��y=x�ľ��x�� ,��AP�ķ���.
,��AP�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)���タ �Ľ��c(di��n)��
�Ľ��c(di��n)��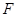 ���c(di��n)
���c(di��n) ������
������ �����c(di��n)�ڒ��タ��. �O(sh��)��ֱ��
�����c(di��n)�ڒ��タ��. �O(sh��)��ֱ��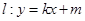 �c���タ�������c(di��n)
�c���タ�������c(di��n) �����c���タ�Ĝ�(zh��n)���ཻ���c(di��n)
�����c���タ�Ĝ�(zh��n)���ཻ���c(di��n) ����
����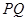 ��ֱ���ĈAӛ��A
��ֱ���ĈAӛ��A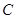 ��
��
��1���� ��ֵ��
��ֵ��
��2���C�����A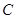 �c
�c �S������c(di��n)��
�S������c(di��n)��
��3��������(bi��o)ƽ�����Ƿ���ڶ��c(di��n) ��ʹ�ÈA
��ʹ�ÈA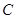 ���^�c(di��n)
���^�c(di��n) �������ڣ����
�������ڣ���� ������(bi��o)���������ڣ��f�����ɣ�
������(bi��o)���������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A +
+ =1(a>b>0),�c(di��n)P��
=1(a>b>0),�c(di��n)P�� a,
a, a���ڙE�A��.
a���ڙE�A��.
(1)��E�A���x����;
(2)�O(sh��)A��E�A������c(di��n),O������(bi��o)ԭ�c(di��n),���c(di��n)Q�ڙE�A���ҝM��|AQ|=|AO|,��ֱ��OQ��б�ʵ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�A �ĈA��������(bi��o)ԭ�c(di��n)O����ǡ���cֱ��
�ĈA��������(bi��o)ԭ�c(di��n)O����ǡ���cֱ�� ����.
����.
(1)��A�Ę�(bi��o)��(zh��n)���̣�
(2)�O(sh��)�c(di��n)A��A��һ���c(di��n)��AN
 �S��N������c(di��n)Q�M��
�S��N������c(di��n)Q�M�� ������m����㳣��(sh��)����ԇ����c(di��n)
������m����㳣��(sh��)����ԇ����c(di��n) ��܉�E����
��܉�E���� .
.
(3)�ڣ�2���ĽY(ji��)Փ�£���(d��ng) �r���õ����c(di��n)Q��܉�E����C���c
�r���õ����c(di��n)Q��܉�E����C���c ��ֱ��ֱ��
��ֱ��ֱ�� �c����C���� B��D���c(di��n)����
�c����C���� B��D���c(di��n)���� ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D���E�A �^�c(di��n)P(1,
�^�c(di��n)P(1, 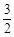 )�������ҽ��c(di��n)�քe��F1,F2,�x����e��
)�������ҽ��c(di��n)�քe��F1,F2,�x����e�� , M, N��ֱ��x��4�ϵăɂ����c(di��n)����
, M, N��ֱ��x��4�ϵăɂ����c(di��n)���� ��
�� ��0.
��0.
��1����E�A�ķ��̣�
��2����MN����Сֵ��
��3����MN��ֱ���ĈAC�Ƿ��^���c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�o���E�AC: +
+ =1(a>b>0),�Q�A����ԭ�c(di��n)O,�돽��
=1(a>b>0),�Q�A����ԭ�c(di��n)O,�돽�� �ĈA�ǙE�AC�ġ���(zh��n)�A��.���E�AC��һ�����c(di��n)��F(
�ĈA�ǙE�AC�ġ���(zh��n)�A��.���E�AC��һ�����c(di��n)��F( ,0),����S�ϵ�һ�����c(di��n)��F�ľ��x��
,0),����S�ϵ�һ�����c(di��n)��F�ľ��x�� .
.
(1)��E�AC�ķ��̺��䡰��(zh��n)�A���ķ���.
(2)�c(di��n)P�ǙE�AC�ġ���(zh��n)�A���ϵ�һ�����c(di��n),�^���c(di��n)P��ֱ��l1,l2ʹ��l1,l2�c�E�AC��ֻ��һ�����c(di��n),��l1,l2�քe���䡰��(zh��n)�A�����c(di��n)M,N.
�ٮ�(d��ng)P�顰��(zh��n)�A���cy�S�����S�Ľ��c(di��n)�r,��l1,l2�ķ���;
�����C:|MN|�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D��ֱ�� �����タ
�����タ ����֪�c(di��n)
����֪�c(di��n) �ڒ��タ
�ڒ��タ �ϣ��Ғ��タ
�ϣ��Ғ��タ �ϵ��c(di��n)��ֱ��
�ϵ��c(di��n)��ֱ�� �ľ��x����Сֵ��
�ľ��x����Сֵ�� ��
��
��1����ֱ�� �����タ
�����タ �ķ��̣�
�ķ��̣�
��2���^�c(di��n) ����һֱ��������(j��ng)�^�c(di��n)
����һֱ��������(j��ng)�^�c(di��n) ���c���タ
���c���タ ����
���� ��
�� ���c(di��n)��ֱ��
���c(di��n)��ֱ�� �cֱ��
�cֱ�� �ཻ���c(di��n)
�ཻ���c(di��n) ��ӛֱ��
��ӛֱ�� ��
�� ��
�� ��б�ʷքe��
��б�ʷքe�� ��
�� ��
��  �������Ƿ���ڌ�(sh��)��(sh��)
�������Ƿ���ڌ�(sh��)��(sh��) ��ʹ��
��ʹ�� �������ڣ�ԇ���
�������ڣ�ԇ��� ��ֵ���������ڣ�Ո�f�����ɣ�
��ֵ���������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
���E�A ��1�Ľ�����2����E�A�ϵ�һ�c(di��n)���ɂ����c(di��n)�ľ��x֮�ͣ�
��1�Ľ�����2����E�A�ϵ�һ�c(di��n)���ɂ����c(di��n)�ľ��x֮�ͣ�
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com