
(08年遼寧卷理)設函數![]() .
.
⑴求![]() 的單調區間和極值;
的單調區間和極值;
⑵是否存在實數![]() ,使得關于
,使得關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ?若存在,求
?若存在,求![]() 的取值范圍;若不存在,試說明理由.
的取值范圍;若不存在,試說明理由.
說明:本小題主要考查函數的導數,單調性,極值,不等式等基礎知識,考查綜合利用數學知識分析問題、解決問題的能力.滿分14分.
解析:(Ⅰ)![]() .?????????????????????????? 2分
.?????????????????????????? 2分
故當![]() 時,
時,![]() ,
,
![]() 時,
時,![]() .
.
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.??????????????????????????????????????????? 4分
單調遞減.??????????????????????????????????????????? 4分
由此知![]() 在
在![]() 的極大值為
的極大值為![]() ,沒有極小值.????????????????????????????? 6分
,沒有極小值.????????????????????????????? 6分
(Ⅱ)()當![]() 時,
時,
由于![]() ,
,
故關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() .????????????????????????????????????????????? 10分
.????????????????????????????????????????????? 10分
()當![]() 時,由
時,由![]() 知
知![]() ,其中
,其中![]() 為正整數,且有
為正整數,且有
![]() .????????????????????????????????????? 12分
.????????????????????????????????????? 12分
又![]() 時,
時,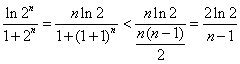 .
.
且![]() .
.
取整數![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,
,
則![]() ,
,
即當![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 的解集不是
的解集不是![]() .
.
綜合()()知,存在![]() ,使得關于
,使得關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ,且
,且![]() 的取值范圍為
的取值范圍為![]() . 14分
. 14分


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com