設函數(shù)
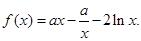
(Ⅰ)若
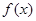
在
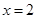
時有極值,求實數(shù)
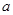
的值和
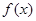
的單調區(qū)間;
(Ⅱ)若
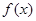
在定義域上是增函數(shù),求實數(shù)
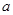
的取值范圍.
(1)

;遞增區(qū)間為:
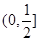
和
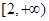
,遞減區(qū)間為:
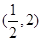
;(2)
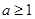
.
試題分析:(1)
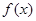
在
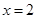
時有極值,意味著
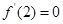
,可求解
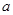
的值.再利用
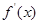
大于零或小于零求函數(shù)的單調區(qū)間;(2)轉化成
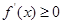
在定義域內恒成立問題求解
試題解析:(Ⅰ)
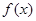
在
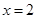
時有極值,
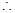
有
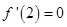
, 2分
又
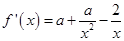
,
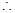
有
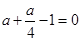
,
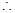

4分
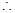
有
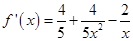
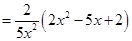
,
由
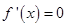
有
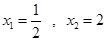
, 6分
又
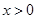
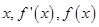
關系有下表
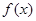
的遞增區(qū)間為
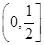
和
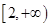
, 遞減區(qū)間為
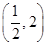
9分
(Ⅱ)若
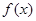
在定義域上是增函數(shù),則
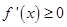
在
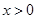
時恒成立, 10分
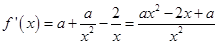
,
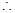
需
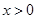
時
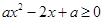
恒成立,
化為
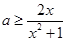
恒成立,
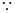
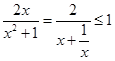
,
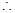
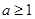
. 14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
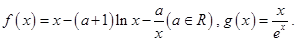
(I)求f(x)的單調區(qū)間;
(II)當
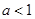
時,若存在
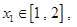
使得對任意的
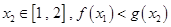
恒成立,求
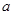
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
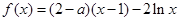
,
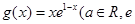
為自然對數(shù)的底數(shù)).
(Ⅰ)當
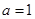
時,求
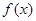
的單調區(qū)間;
(Ⅱ)若函數(shù)
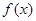
在
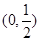
上無零點,求
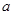
最小值;
(Ⅲ)若對任意給定的
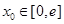
,在
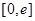
上總存在兩個不同的
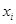
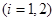
),使
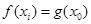
成立,求
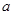
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
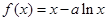
,
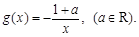
(Ⅰ)若
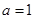
,求函數(shù)
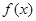
的極值;
(Ⅱ)設函數(shù)
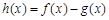
,求函數(shù)
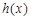
的單調區(qū)間;
(Ⅲ)若在區(qū)間
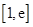
(
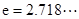
)上存在一點
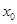
,使得
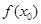
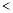
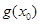
成立,求
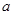
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
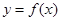
是定義在數(shù)集
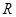
上的奇函數(shù),且當
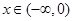
時,
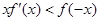
成立,若
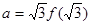
,
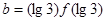
,
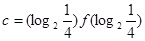
,則
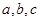
的大小關系是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
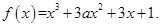
(I)當
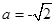
時,討論
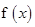
的單調性;
(II)若
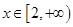
時,
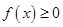
,求
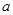
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
函數(shù)
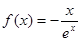
(
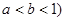
,則 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
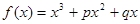
與
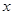
軸切于
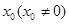
點,且極小值為
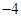
,則
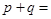
( )
查看答案和解析>>

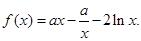
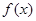 在
在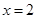 時有極值,求實數(shù)
時有極值,求實數(shù)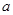 的值和
的值和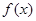 的單調區(qū)間;
的單調區(qū)間; 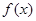 在定義域上是增函數(shù),求實數(shù)
在定義域上是增函數(shù),求實數(shù)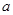 的取值范圍.
的取值范圍.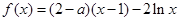 ,
,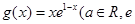 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).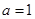 時,求
時,求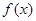 的單調區(qū)間;
的單調區(qū)間;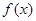 在
在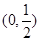 上無零點,求
上無零點,求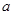 最小值;
最小值;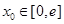 ,在
,在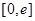 上總存在兩個不同的
上總存在兩個不同的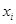
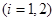 ),使
),使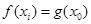 成立,求
成立,求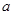 的取值范圍.
的取值范圍.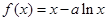 ,
,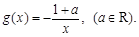
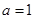 ,求函數(shù)
,求函數(shù)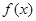 的極值;
的極值;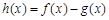 ,求函數(shù)
,求函數(shù)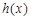 的單調區(qū)間;
的單調區(qū)間;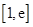 (
(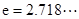 )上存在一點
)上存在一點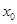 ,使得
,使得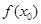
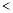
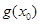 成立,求
成立,求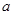 的取值范圍.
的取值范圍.