
如圖,橢圓的中心在原點,其左焦點![]() 與拋物線
與拋物線![]() 的焦點重合,過
的焦點重合,過![]() 的直線
的直線![]() 與橢圓交于A、B兩點,與拋物線交于C、D兩點.當直線
與橢圓交于A、B兩點,與拋物線交于C、D兩點.當直線![]() 與x軸垂直時,
與x軸垂直時,![]() .
.
(Ⅰ)求橢圓的方程;
(II)求過點O、![]() ,并且與橢圓的左準線相切的圓的方程;
,并且與橢圓的左準線相切的圓的方程;
(Ⅲ)求![]() 的最大值和最小值.
的最大值和最小值.

(Ⅰ)![]()
(Ⅱ)![]()
(Ⅲ)最大值![]() ,最小值
,最小值![]()
(Ⅰ)由拋物線方程,得焦點![]() .
.
設橢圓的方程:![]() .
.
解方程組 得C(-1,2),D(1,-2).
得C(-1,2),D(1,-2).
由于拋物線、橢圓都關于x軸對稱,
∴![]() ,
,![]() , ∴
, ∴![]() . …………2分
. …………2分
∴![]() 又
又![]() ,
,
因此,![]() ,解得
,解得![]() 并推得
并推得![]() .
.
故橢圓的方程為![]() . …………4分
. …………4分
(Ⅱ)![]() ,
,
![]() 圓過點O、
圓過點O、![]() ,
,
![]() 圓心M在直線
圓心M在直線![]() 上.
上.
設![]() 則圓半徑,由于圓與橢圓的左準線相切,
則圓半徑,由于圓與橢圓的左準線相切,
∴![]()
由![]() 得
得![]() 解得
解得![]()
![]() 所求圓的方程為
所求圓的方程為![]() …………………………8分
…………………………8分
(Ⅲ) 由![]()
①若![]() 垂直于
垂直于![]() 軸,則
軸,則![]() ,
,
![]() ,
,
![]() …………………………………………9分
…………………………………………9分
②若![]() 與
與![]() 軸不垂直,設直線
軸不垂直,設直線![]() 的斜率為
的斜率為![]() ,則直線
,則直線![]() 的方程為
的方程為
![]()
由![]() 得
得 ![]()
![]() ,
,![]() 方程有兩個不等的實數根.
方程有兩個不等的實數根.
設![]() ,
,![]() .
.
![]() ,
, ![]() ………………………………11分
………………………………11分
![]()
![]()
![]()
![]()
=![]()
![]()
![]() ,所以當直線
,所以當直線![]() 垂于
垂于![]() 軸時,
軸時,![]() 取得最大值
取得最大值![]()
當直線![]() 與
與![]() 軸重合時,
軸重合時,![]() 取得最小值
取得最小值![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
 如圖,橢圓的中心在原點,F為橢圓的左焦點,B為橢圓的一個頂點,過點B作與FB垂直的直線BP交x軸于P點,且橢圓的長半軸長a和短半軸長b是關于x的方程3x2-3
如圖,橢圓的中心在原點,F為橢圓的左焦點,B為橢圓的一個頂點,過點B作與FB垂直的直線BP交x軸于P點,且橢圓的長半軸長a和短半軸長b是關于x的方程3x2-3| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,橢圓的中心在原點,長軸AA1在x軸上.以A、A1為焦點的雙曲線交橢圓于C、D、D1、C1四點,且|CD|=![]() |AA1|.橢圓的一條弦AC交雙曲線于E,設
|AA1|.橢圓的一條弦AC交雙曲線于E,設![]() ,當
,當![]() 時,求雙曲線的離心率e的取值范圍.
時,求雙曲線的離心率e的取值范圍.

查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三下學期質量檢測數學試卷 題型:解答題
如圖,橢圓 的中心在原點,焦點在
的中心在原點,焦點在 軸上,
軸上, 分別是橢圓
分別是橢圓 的左、右焦點,
的左、右焦點, 是橢圓短軸的一個端點,過
是橢圓短軸的一個端點,過 的直線
的直線 與橢圓交于
與橢圓交于 兩點,
兩點, 的面積為
的面積為 ,
, 的周長為
的周長為 .
.
(1)求橢圓 的方程;
的方程;
(2)設點 的坐標為
的坐標為 ,是否存在橢圓上的點
,是否存在橢圓上的點 及以
及以 為圓心的一個圓,使得該圓與直線
為圓心的一個圓,使得該圓與直線 都相切,如存在,求出
都相切,如存在,求出 點坐標及圓的方程,如不存在,請說明理由.
點坐標及圓的方程,如不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省南京市白下區高三二模數學試卷 題型:解答題
(本小題滿分15分)
如圖,橢圓 的中心在原點,焦點在
的中心在原點,焦點在 軸上,
軸上, 分別是橢圓
分別是橢圓 的左、右焦點,
的左、右焦點, 是橢圓短軸的一個端點,過
是橢圓短軸的一個端點,過 的直線
的直線 與橢圓交于
與橢圓交于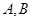 兩點,
兩點, 的面積為
的面積為 ,
, 的周長為
的周長為 .
.

(1)求橢圓 的方程;
的方程;
(2)設點 的坐標為
的坐標為 ,是否存在橢圓上的點
,是否存在橢圓上的點 及以
及以 為圓心的一個圓,使得該圓與直線
為圓心的一個圓,使得該圓與直線 都相切,如存在,求出
都相切,如存在,求出 點坐標及圓的方程,如不存在,請說明理由.
點坐標及圓的方程,如不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com