
(本題滿分18分,第1小題4分,第2小題6分,第3小題8分)
已知數(shù)列{an}滿足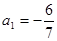 ,
,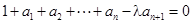 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),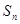 為數(shù)列{an}的前
為數(shù)列{an}的前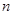 項(xiàng)和.
項(xiàng)和.
(1) 若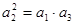 ,求
,求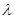 的值;
的值;
(2) 求數(shù)列{an}的通項(xiàng)公式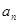 ;
;
(3) 當(dāng)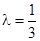 時(shí),數(shù)列{an}中是否存在三項(xiàng)構(gòu)成等差數(shù)列,若存在,請(qǐng)求出此三項(xiàng);若不存在,請(qǐng)說(shuō)明理由.
時(shí),數(shù)列{an}中是否存在三項(xiàng)構(gòu)成等差數(shù)列,若存在,請(qǐng)求出此三項(xiàng);若不存在,請(qǐng)說(shuō)明理由.
(1)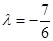 ;(2)數(shù)列{an}中存在a1、a2、a3或a3、a2、a1成等差數(shù)列。
;(2)數(shù)列{an}中存在a1、a2、a3或a3、a2、a1成等差數(shù)列。
【解析】
試題分析:(1) 令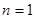 ,得到
,得到 ,令
,令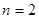 ,得到
,得到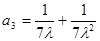 。…………2分
。…………2分
由 ,計(jì)算得
,計(jì)算得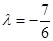 .……………………………………………………4分
.……………………………………………………4分
(2) 由題意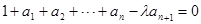 ,可得:
,可得:
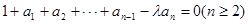 ,所以有
,所以有
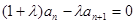
 ,又
,又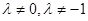 ,……………………5分
,……………………5分
得到: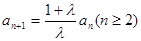 ,故數(shù)列
,故數(shù)列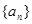 從第二項(xiàng)起是等比數(shù)列。……………7分
從第二項(xiàng)起是等比數(shù)列。……………7分
又因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013031412302175769897/SYS201303141231136639982286_DA.files/image003.png">,所以n≥2時(shí),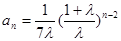 ……………………………8分
……………………………8分
所以數(shù)列{an}的通項(xiàng)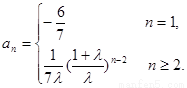 …………………………………10分
…………………………………10分
(3) 因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013031412302175769897/SYS201303141231136639982286_DA.files/image016.png"> 所以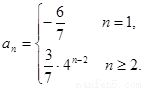 ……………………………………11分
……………………………………11分
假設(shè)數(shù)列{an}中存在三項(xiàng)am、ak、ap成等差數(shù)列,
①不防設(shè)m>k>p≥2,因?yàn)楫?dāng)n≥2時(shí),數(shù)列{an}單調(diào)遞增,所以2ak=am+ap
即:2´(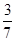 )´4k–2 =
)´4k–2 = 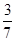 ´4m–2 +
´4m–2 + 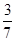 ´4p–2,化簡(jiǎn)得:2´4k - p= 4m–p+1
´4p–2,化簡(jiǎn)得:2´4k - p= 4m–p+1
即22k–2p+1=22m–2p+1,若此式成立,必有:2m–2p=0且2k–2p+1=1,
故有:m=p=k,和題設(shè)矛盾………………………………………………………………14分
②假設(shè)存在成等差數(shù)列的三項(xiàng)中包含a1時(shí),
不妨設(shè)m=1,k>p≥2且ak>ap,所以2ap = a1+ak ,
2´(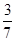 )´4p–2 = –
)´4p–2 = –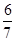 + (
+ (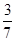 )´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
)´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
因?yàn)?i>k > p ≥ 2,所以當(dāng)且僅當(dāng)k=3且p=2時(shí)成立………………………………………16分
因此,數(shù)列{an}中存在a1、a2、a3或a3、a2、a1成等差數(shù)列……………………………18分
考點(diǎn):等差數(shù)列的性質(zhì);數(shù)列通項(xiàng)公式的求法;數(shù)列的遞推式。
點(diǎn)評(píng):本題主要考查了利用數(shù)列的遞推公式求解數(shù)列的通項(xiàng)公式,還考查了一定的邏輯運(yùn)算與推理的能力及考查了學(xué)生通過(guò)已知條件分析問(wèn)題和解決問(wèn)題的能力.題目較難。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(本題滿分18分,第(1)小題4分,第(2)小題6分,第(3)小題8分)
在平行四邊形![]() 中,已知過(guò)點(diǎn)
中,已知過(guò)點(diǎn)![]() 的直線與線段
的直線與線段![]() 分別相交于點(diǎn)
分別相交于點(diǎn)![]() 。若
。若![]() 。
。
(1)求證:![]() 與
與![]() 的關(guān)系為
的關(guān)系為![]() ;
;
(2)設(shè)![]() ,定義函數(shù)
,定義函數(shù)![]() ,點(diǎn)列
,點(diǎn)列![]() 在函數(shù)
在函數(shù)![]() 的圖像上,且數(shù)列
的圖像上,且數(shù)列![]() 是以首項(xiàng)為1,公比為
是以首項(xiàng)為1,公比為![]() 的等比數(shù)列,
的等比數(shù)列,![]() 為原點(diǎn),令
為原點(diǎn),令![]() ,是否存在點(diǎn)
,是否存在點(diǎn)![]()
![]() ,使得
,使得![]() ?若存在,請(qǐng)求出
?若存在,請(qǐng)求出![]() 點(diǎn)坐標(biāo);若不存在,請(qǐng)說(shuō)明理由。
點(diǎn)坐標(biāo);若不存在,請(qǐng)說(shuō)明理由。
(3)設(shè)函數(shù)![]() 為
為![]() 上偶函數(shù),當(dāng)
上偶函數(shù),當(dāng)![]() 時(shí)
時(shí)![]() ,又函數(shù)
,又函數(shù)![]() 圖象關(guān)于直線
圖象關(guān)于直線![]() 對(duì)稱, 當(dāng)方程
對(duì)稱, 當(dāng)方程![]() 在
在![]() 上有兩個(gè)不同的實(shí)數(shù)解時(shí),求實(shí)數(shù)
上有兩個(gè)不同的實(shí)數(shù)解時(shí),求實(shí)數(shù)![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012屆上海市崇明中學(xué)高三第一學(xué)期期中考試試題數(shù)學(xué) 題型:解答題
(本題滿分18分,第(1)小題4分,第(2)小題6分,第(3)小題8分)
對(duì)于數(shù)列 ,如果存在一個(gè)正整數(shù)
,如果存在一個(gè)正整數(shù) ,使得對(duì)任意的
,使得對(duì)任意的 (
( )都有
)都有 成立,那么就把這樣一類數(shù)列
成立,那么就把這樣一類數(shù)列 稱作周期為
稱作周期為 的周期數(shù)列,
的周期數(shù)列, 的最小值稱作數(shù)列
的最小值稱作數(shù)列 的最小正周期,以下簡(jiǎn)稱周期。例如當(dāng)
的最小正周期,以下簡(jiǎn)稱周期。例如當(dāng) 時(shí)
時(shí) 是周期為
是周期為 的周期數(shù)列,當(dāng)
的周期數(shù)列,當(dāng)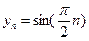 時(shí)
時(shí) 是周期為
是周期為 的周期數(shù)列。
的周期數(shù)列。
(1)設(shè)數(shù)列 滿足
滿足 (
( ),
), (
( 不同時(shí)為0),且數(shù)列
不同時(shí)為0),且數(shù)列 是周期為
是周期為 的周期數(shù)列,求常數(shù)
的周期數(shù)列,求常數(shù) 的值;
的值;
(2)設(shè)數(shù)列 的前
的前 項(xiàng)和為
項(xiàng)和為 ,且
,且 .
.
①若 ,試判斷數(shù)列
,試判斷數(shù)列 是否為周期數(shù)列,并說(shuō)明理由;
是否為周期數(shù)列,并說(shuō)明理由;
②若 ,試判斷數(shù)列
,試判斷數(shù)列 是否為周期數(shù)列,并說(shuō)明理由;
是否為周期數(shù)列,并說(shuō)明理由;
(3)設(shè)數(shù)列 滿足
滿足 (
( ),
), ,
,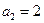 ,
, ,數(shù)列
,數(shù)列 的前
的前 項(xiàng)和為
項(xiàng)和為 ,試問(wèn)是否存在
,試問(wèn)是否存在 ,使對(duì)任意的
,使對(duì)任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范圍;不存在, 說(shuō)明理由;
的取值范圍;不存在, 說(shuō)明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年上海市高三第一學(xué)期期中考試試題數(shù)學(xué) 題型:解答題
(本題滿分18分,第(1)小題4分,第(2)小題6分,第(3)小題8分)
對(duì)于數(shù)列 ,如果存在一個(gè)正整數(shù)
,如果存在一個(gè)正整數(shù) ,使得對(duì)任意的
,使得對(duì)任意的 (
( )都有
)都有 成立,那么就把這樣一類數(shù)列
成立,那么就把這樣一類數(shù)列 稱作周期為
稱作周期為 的周期數(shù)列,
的周期數(shù)列, 的最小值稱作數(shù)列
的最小值稱作數(shù)列 的最小正周期,以下簡(jiǎn)稱周期。例如當(dāng)
的最小正周期,以下簡(jiǎn)稱周期。例如當(dāng) 時(shí)
時(shí) 是周期為
是周期為 的周期數(shù)列,當(dāng)
的周期數(shù)列,當(dāng) 時(shí)
時(shí) 是周期為
是周期為 的周期數(shù)列。
的周期數(shù)列。
(1)設(shè)數(shù)列 滿足
滿足 (
( ),
), (
(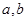 不同時(shí)為0),且數(shù)列
不同時(shí)為0),且數(shù)列 是周期為
是周期為 的周期數(shù)列,求常數(shù)
的周期數(shù)列,求常數(shù) 的值;
的值;
(2)設(shè)數(shù)列 的前
的前 項(xiàng)和為
項(xiàng)和為 ,且
,且 .
.
①若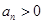 ,試判斷數(shù)列
,試判斷數(shù)列 是否為周期數(shù)列,并說(shuō)明理由;
是否為周期數(shù)列,并說(shuō)明理由;
②若 ,試判斷數(shù)列
,試判斷數(shù)列 是否為周期數(shù)列,并說(shuō)明理由;
是否為周期數(shù)列,并說(shuō)明理由;
(3)設(shè)數(shù)列 滿足
滿足 (
( ),
),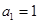 ,
,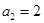 ,
, ,數(shù)列
,數(shù)列 的前
的前 項(xiàng)和為
項(xiàng)和為 ,試問(wèn)是否存在
,試問(wèn)是否存在 ,使對(duì)任意的
,使對(duì)任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范圍;不存在,
說(shuō)明理由;
的取值范圍;不存在,
說(shuō)明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年上海市十三校高三上學(xué)期第一次聯(lián)考試題文科數(shù)學(xué) 題型:解答題
(本題滿分18分,第1小題滿分5分,第2小題滿分5分,第3小題滿分8分)
已知函數(shù) ,其中
,其中 .
.
(1)當(dāng) 時(shí),設(shè)
時(shí),設(shè) ,
, ,求
,求 的解析式及定義域;
的解析式及定義域;
(2)當(dāng) ,
, 時(shí),求
時(shí),求 的最小值;
的最小值;
(3)設(shè) ,當(dāng)
,當(dāng) 時(shí),
時(shí), 對(duì)任意
對(duì)任意 恒成立,求
恒成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010年上海市徐匯區(qū)高三第二次模擬考試數(shù)學(xué)卷(文) 題型:解答題
(本題滿分18分;第(1)小題5分,第(2)小題5分,第(3)小題8分)
設(shè)數(shù)列 是等差數(shù)列,且公差為
是等差數(shù)列,且公差為 ,若數(shù)列
,若數(shù)列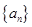 中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱該數(shù)列是“封閉數(shù)列”.
中任意(不同)兩項(xiàng)之和仍是該數(shù)列中的一項(xiàng),則稱該數(shù)列是“封閉數(shù)列”.
(1)若 ,求證:該數(shù)列是“封閉數(shù)列”;
,求證:該數(shù)列是“封閉數(shù)列”;
(2)試判斷數(shù)列 是否是“封閉數(shù)列”,為什么?
是否是“封閉數(shù)列”,為什么?
(3)設(shè) 是數(shù)列
是數(shù)列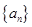 的前
的前 項(xiàng)和,若公差
項(xiàng)和,若公差 ,試問(wèn):是否存在這樣的“封閉數(shù)列”,使
,試問(wèn):是否存在這樣的“封閉數(shù)列”,使 ;若存在,求
;若存在,求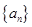 的通項(xiàng)公式,若不存在,說(shuō)明理由.
的通項(xiàng)公式,若不存在,說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com