
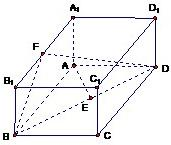
 ��D����֪�L���wABCD-A1B1C1D1��AB=2��AA1=1��ֱ��BD�cƽ��AA1B1B���ɵĽǞ�30�㣬AE��ֱBD��E��F(xi��n)��A1B1�����c��
��D����֪�L���wABCD-A1B1C1D1��AB=2��AA1=1��ֱ��BD�cƽ��AA1B1B���ɵĽǞ�30�㣬AE��ֱBD��E��F(xi��n)��A1B1�����c��| �������ⷨһ�� �ں���ֱ���cƽ�洹ֱ��ֱ�ėl�������������F�����_�У����Խ������gֱ������(bi��o)ϵ���O(sh��)��������⣮������}�У��҂�������A������(bi��o)ԭ�c���քe��AB��AD��AA1��x��y��z�S���������gֱ������(bi��o)ϵO-xyz���@�N�ⷨ�ĺ�̎���ǣ��ٽ��}�^�����^���õ����g�����ж����������桢��������λ�õ����P(gu��n)����������@Щ������������������Q���ڼ�ʹ���w���Բ�һЩ�ČW(xu��)��Ҳ���������������ֻ�讋���݈D�Խ�������(bi��o)ϵ���^�����P(gu��n)�c��λ�ü��ɣ� ��I����
��II����֪ƽ��AA1B��һ��������
��III���cA��ƽ��BDF�ľ��x����
�ⷨ���� ��I������ֱ�����ɵĽǣ�Ҳ�������m��(d��ng)?sh��)�ƽ�ƣ��Ѯ���ֱ���D(zhu��n)�����ֱཻ����Ȼ�������P(gu��n)���������н������һ����Ҷ����������Ľǣ�ƽ�ƕr��Ҫ�Ǹ���(j��)��λ�������c�l�����������������߅�Σ������εȣ��B��B1D1���^F��B1D1�Ĵ����������K���tFK��AE�����BFK�鮐��ֱ��BF�cAE���ɵĽǣ� ��II������ǵĶ����P(gu��n)�I�����ҳ�����ƽ��ǣ���(g��u)��ƽ��dz��õķ���������������������DA����AA2B����A��BF�Ĵ���AG�������G���B��DG��������������֪BG��DG�����AGD����ƽ��BDF�cƽ��AA1B���ɶ���ǵ�ƽ��ǣ� ��III�������w���У����c��ƽ��ľ��x��һ����Ҋ���}�ͣ�ͬ�r��ֱ����ƽ��ľ��x��ƽ��ƽ���g�ľ��x�������w���w�eҲ���D(zhu��n)�������c��ƽ��ľ��x���ң�������һ���^ԓ�c��ƽ���c��֪ƽ�洹ֱ��Ȼ���^ԓ�c���佻���Ĵ������t���c��ƽ��Ĵ����Σ��ɣ�II��֪ƽ��AFD��ƽ��BDF�cƽ��AA1B���ɶ���_��ƽ������ڵ�ƽ�����AFD����BDF����Rt��ADF����A��AH��DF��H���tAH�����cA��ƽ��BDF�ľ��x�� | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
���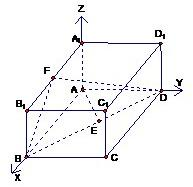 �⣺��һ�����L���wABCD-A1B1C1D1�У���AB����ֱ����x�S��AD����ֱ����y �⣺��һ�����L���wABCD-A1B1C1D1�У���AB����ֱ����x�S��AD����ֱ����y�S��AA1����ֱ����z�S�������gֱ������(bi��o)ϵ��D�� ����֪AB=2��AA1=1���ɵ�A��0��0��0����B��2��0��0����F(xi��n)��1��0��1���� ��AD��ƽ��AA1B1B���Ķ�BD�cƽ��AA1B1B���ɵĽǼ����DBA=30�㣬 ��AB=2��AE��BD��AE=1��AD=
�Ķ���E(
��I����
��cos��
������ֱ��AE��B���ɵĽǞ�arccos
��II����֪ƽ��AA1B��һ��������
�O(sh��)
��
ȡ
��ƽ��BDF�cƽ��AA1B���ɶ���ǣ��J�ǣ���С��arccos
��III���cA��ƽ��BDF�ľ��x����
���Ծ��xd=||
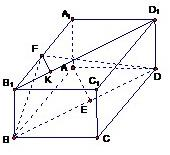 �����cA��ƽ��BDF�ľ��x��
�ⷨ������I���B��B1D1���^F��B1D1�Ĵ����� �����K����BB1�c�ɵ���ABCD��A1B1C1D1����ֱ�� ��
��
���FK��AE�����BFK�鮐��ֱ��BF�cAE���ɵĽǣ� �B��BK����FK����BDD1B1��FK��BK�� �Ķ���BKF��Rt���� ��Rt��B1KF��Rt��B1D1A1�У� ��
��FK=
��BF=
�ஐ��ֱ��BF�cAE���ɵĽǞ�arccos
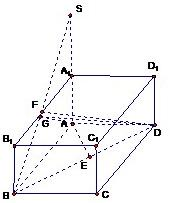 ��II������DA����AA2B����A��BF�Ĵ���AG�������G�� �B��DG��������������֪BG��DG�� ���AGD����ƽ��BDF�cƽ��AA1B���ɶ���ǵ�ƽ��ǣ� �ҡ�DAG=90�㣬��ƽ��AA1B�У����LBF�cAA1���� �cS����F��A2B1�����c��A1F��=
��SA=2A1A=2=AB����Rt��BAS�����ֱ�������Σ� ����G�c��б߅SB�����cF����F��G�غϣ� ��AG=AF=
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||