已知函數(shù)

的定義域為R,對任意
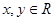
,均有
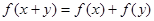
,且對任意
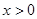
都有
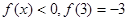
.
(1)試證明:函數(shù)

在R上是單調(diào)函數(shù);
(2)判斷

的奇偶性,并證明;
(3)解不等式
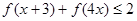
;
(4)試求函數(shù)

在
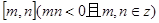
上的值域.
解:(1)任取
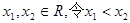
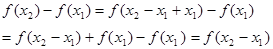
………………2分
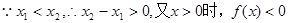
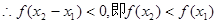
∴

在R上是單調(diào)減函數(shù). ……………… 4分
(2)
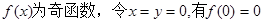
……………… 5分
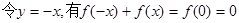
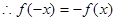
……………… 7分
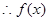
為奇函數(shù) ……………… 8分
(3)
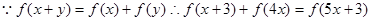
又
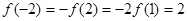
……………… 9分
∴原不等式為:
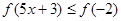
……………… 10分
∵

在R上遞減,
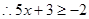
∴不等式的解集為
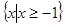
……………… 11分
(4)由題
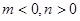
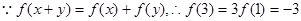
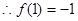
又
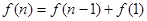
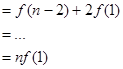
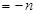
……………… 12分
由(2)知

為奇函數(shù),
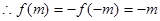
……………… 13分
由(1)知,

在
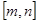
上遞減,
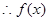
的值域為
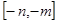
……………… 14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)y=f(x)對任意的實數(shù)ab都有:f(a+b)=f(a)+f(b)﹣1,且x>0時,f(x)>1,
(1)求證:f(x)是R上的增函數(shù);
(2)若f(4)=5,求f(2)的值,并解不等式f(3m2﹣m﹣2)<3.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知:函數(shù)f(x)=
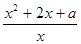
,x
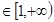
,
(1)當a=-1時,判斷并證明函數(shù)的單調(diào)性并求f(x)的最小值;
(2)若對任意x
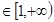
,f(x)>0都成立,試求實數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
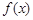
是定義在
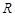
上的奇函數(shù),且當
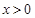
時
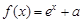
,若
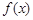
在
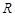
上是單調(diào)函數(shù),則實數(shù)
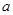
的最小值是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
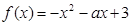
在區(qū)間
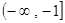
上是增函數(shù),則實數(shù)
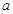
的取值范圍為
____________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
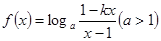
是奇函數(shù),
(1)求
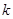
的值;
(2)在(1)的條件下判斷
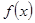
在
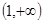
上的單調(diào)性,并運用單調(diào)性的定義予以證明.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
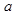
>0且
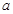
≠1.
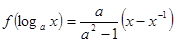
(1)求
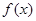
的解析式;
(2)判斷
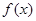
的奇偶性與單調(diào)性;
(3)對于
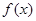
,當
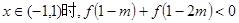
恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
定義域為R的偶函數(shù)f(x)在[0,+∞)是增函數(shù),且

=0,則不等式f(log
4x)>0的解集為 ( )


查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)

在

上的最大值與最小值之和為3,則

的值是
。
查看答案和解析>>

 的定義域為R,對任意
的定義域為R,對任意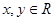 ,均有
,均有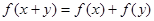 ,且對任意
,且對任意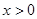 都有
都有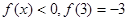 .
. 在R上是單調(diào)函數(shù);
在R上是單調(diào)函數(shù); 的奇偶性,并證明;
的奇偶性,并證明;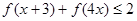 ;
; 在
在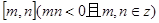 上的值域.
上的值域.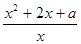 ,x
,x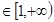 ,
,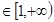 ,f(x)>0都成立,試求實數(shù)a的取值范圍。
,f(x)>0都成立,試求實數(shù)a的取值范圍。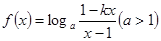 是奇函數(shù),
是奇函數(shù),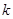 的值;
的值;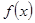 在
在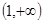 上的單調(diào)性,并運用單調(diào)性的定義予以證明.
上的單調(diào)性,并運用單調(diào)性的定義予以證明.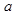 >0且
>0且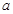 ≠1.
≠1. 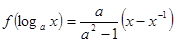
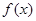 的解析式;
的解析式; 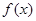 的奇偶性與單調(diào)性;
的奇偶性與單調(diào)性;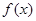 ,當
,當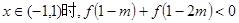 恒成立,求實數(shù)m的取值范圍.
恒成立,求實數(shù)m的取值范圍.