中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

（本小題滿分12分）在中，分別為內角的對邊，且。
（Ⅰ）求角的大小；
（Ⅱ）設函數(shù)，求的最大值，并判斷此時的形狀．
（Ⅰ）（Ⅱ）最大值是，△ABC為等邊三角形．

試題分析：（Ⅰ）在△ABC中，因為b2+c2-a2=bc，由余弦定理 a2= b2+c2-2bccosA 可得cosA=．
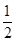
∵ 0<A<π ， （或寫成A是三角形內角） ∴．
（Ⅱ），
∵  ∴ 
∴  
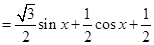
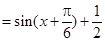
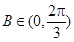
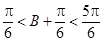
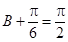
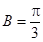
∴當，即時，
有最大值是．
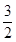
又∵，
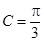
∴ ∴△ABC為等邊三角形．
點評：解三角形時應用正余弦定理實現(xiàn)邊角的互相轉化，三角函數(shù)性質的考查要結合圖像分析求解
練習冊系列答案
相關習題

科目：高中數(shù)學 來源：不詳 題型：解答題

（本小題滿分10分）
在中內角的對邊分別為，且 
（1）求的值；
（2）如果b=4，且a=c,求的面積.

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

平面直角坐標系中，已知頂點A和C,頂點B在橢圓上，則_____

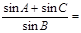
查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

設函數(shù)
（1）設的內角，且為鈍角，求的最小值；
（2）設是銳角的內角，且求的三個內角的大小和AC邊的長。

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

（本小題滿分12分）已知銳角中內角、、的對邊分別為、、，且.
（1）求角的值；
（2）設函數(shù)，圖象上相鄰兩最高點間的距離為，求的取值范圍.

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

為了豎一塊廣告牌，要制造三角型支架，三角形支架如圖所示，要求，長度大于米，且比長米，為了廣告牌的穩(wěn)固，要求的長度越短越好，求最短為多少？

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

在銳角中,若,則的取值范圍是            .

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：填空題

在△中，內角的對邊分別為。若，，則___________。

查看答案和解析>>

科目：高中數(shù)學 來源：不詳 題型：解答題

（本題滿分12分）
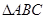
已知的周長為,且
(I)求邊的長；
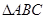
(II)若的面積為,求角C的度數(shù).

查看答案和解析>>

同步練習冊答案