
在平面直角坐標系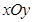 中,已知點
中,已知點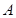
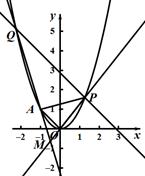
 ,點P是動點,且三角形
,點P是動點,且三角形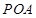 的三邊所在直線
的三邊所在直線
的斜率滿足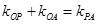 .
.

(1)求點P的軌跡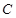 的方程;
的方程;
(2)設Q是軌跡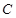 上異于點
上異于點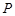 的一個點,若
的一個點,若 ,直線
,直線 與
與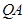 交于點M,探究是否存點P使得
交于點M,探究是否存點P使得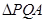 和
和 的面積滿足
的面積滿足 ,若存在,求出點P的坐標;若不存在,說明理由.
,若存在,求出點P的坐標;若不存在,說明理由.
解:(1)設點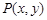 為所求軌跡上的任意一點,由
為所求軌跡上的任意一點,由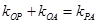 得,
得,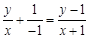 ,
,
整理得 的方程為
的方程為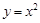 (
(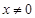 且
且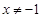 )。……4分(注:不寫范圍扣1分)
)。……4分(注:不寫范圍扣1分)
(2)解法一、設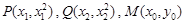 ,
,
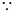
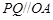 ,
,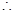
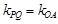 ,
,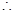
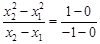 ,即
,即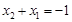 , ………6分
, ………6分
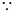
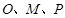 三點共線,
三點共線,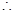
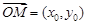 與
與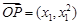 共線,∴
共線,∴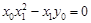 ,
,
由(1)知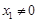 ,故
,故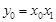 , ………8分
, ………8分
同理,由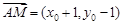 與
與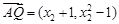 共線,
共線,
∴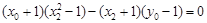 ,即
,即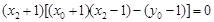 ,
,
由(1)知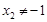 ,故
,故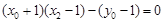 ,…………9分
,…………9分
將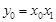 ,
,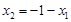 代入上式得
代入上式得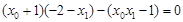 ,
,
整理得 ,由
,由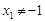 得
得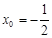 , …………11分
, …………11分
由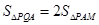 ,得到
,得到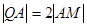 ,因為
,因為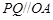 ,所以
,所以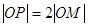 ,
,
由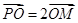 ,得
,得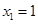 , ∴
, ∴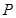 的坐標為
的坐標為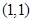 . …………14分
. …………14分
解法二、設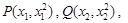 由
由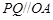 得
得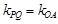 ,
,
故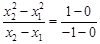 ,即
,即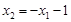 ,
………6分
,
………6分
∴直線OP方程為: ①;
…………8分
①;
…………8分
直線QA的斜率為: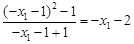 ,
,
∴直線QA方程為: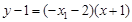 ,即
,即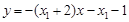 , ② …10分
, ② …10分
聯立①②,得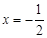 ,∴點M的橫坐標為定值
,∴點M的橫坐標為定值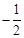 。…………11分
。…………11分
由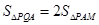 ,得到
,得到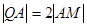 ,因為
,因為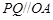 ,所以
,所以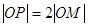 ,
,
由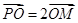 ,得
,得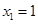 , ∴
, ∴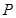 的坐標為
的坐標為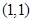 . …………14分
. …………14分
【解析】考查向量知識在幾何中的運用,實際上就是用坐標表示向量,再進行運算;(Ⅱ)的關鍵是確定出點M的橫坐標為定值.
(Ⅰ)設點P(x,y)為所求軌跡上的任意一點,則由kOP+kOA=kPA得從而就可以得到軌跡C的方程;
(2)設出點PQ,M的坐標,然后利用三點共線得到坐標關系,進而再由面積得到點P的坐標。


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
| π | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com