(本題滿分12分)在斜三角形
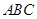
中,內角
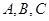
的對邊分別為
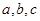
。若
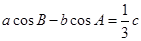
。(1)證明:

;(2)求
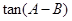
的最大值。
(1)見解析;(2)
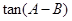
的最大值為

。
試題分析:本題考查正弦定理、兩角和與兩角差的三角函數(shù)公式、內角和定理以及運用均值不等式求函數(shù)的最值。
(1)由
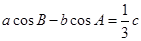
和正弦定理得

(1分)。
又因為

(2分),
故

(3分),
于是

(4分),
故

(5分)。
由于

都不是直角,故

,兩邊除以

得

(6分)。
(2)由(1):

,故

(7分)

(8分)。
再由

知

(9分),
故

(10分)。
因

(11分),
故
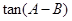
的最大值為

(12分)。
點評:綜合性較強,不但對正弦定理、兩角和與差的三角函數(shù)進行了考查,而且考查了均值定理的應用。應用均值定理,應遵循“一正、二定、三相等”的方法要求,其中“三相等”最易被忽視。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分10分)在

中,

,

,

分別是三內角A,B,C所對的三邊,已知

.
(1)求角A的大小;
(2)若

,試判斷

的形狀.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)設

,

,

且

,
(Ⅰ)求

的值;
(Ⅱ)設

三內角

所對邊分別為

且

,求

在

上的值域.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在△ABC中,角A、B、C所對的邊分別是a、b、c,且
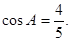
(1)求
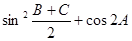
的值;(2)若

的值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分10分)如圖,△ABC中,

,點D 在BC邊上,∠ADC=45°。
(1)求

的大小;(2)求AD的長。

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在△ABC中,角A、B、C所對的邊分別為a、b、c,若(2b
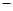
c)cosA=acosC,則角A=
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知
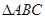
,內角
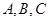
所對的邊分別為
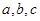
,且滿足下列三個條件:①
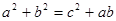
②
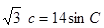
③
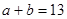
求: (1) 內角
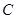
和邊長
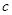
的大小; (2)
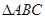
的面積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在三角形ABC中,A=120°,AB=5,BC=7,則

的值為____
________。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在
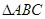
,角
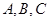
所對應的邊為
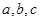
.
(1)若
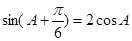
,求
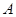
的值;
(2)若
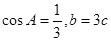
,求
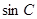
的值.
查看答案和解析>>

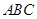 中,內角
中,內角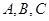 的對邊分別為
的對邊分別為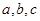 。若
。若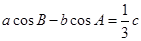 。(1)證明:
。(1)證明: ;(2)求
;(2)求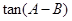 的最大值。
的最大值。 閱讀快車系列答案
閱讀快車系列答案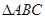 ,內角
,內角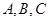 所對的邊分別為
所對的邊分別為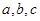 ,且滿足下列三個條件:①
,且滿足下列三個條件:①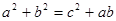 ②
②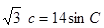 ③
③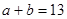
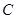 和邊長
和邊長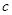 的大小; (2)
的大小; (2) 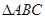 的面積.
的面積.