解關于x的不等式：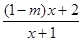
≤
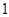
詳見解析
解析試題分析：首先移項化簡，得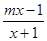
≥
，對m進行分類討論，分別討論m=0，m>0，m<0的情形，即可得到結果．．
試題解析：解：原不等式化為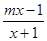≥ (1分)
①當m=0時，原不等式化為－x-1>0,解集為（-∞，-1） (3分)
②當m>0時，原不等式化為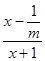
≥，又
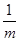> -1
∴原不等式的解集為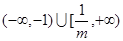
(5分)
③當m<0時，原不等式化為≤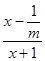
當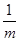< -1即-1<m<0時，所以原不等式的解集為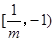
當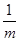=-1即 m=-1時，所以原不等式的解集為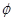
當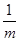> -1即m<-1時，所以原不等式的解集為
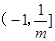(11分)
綜上所述，當m=0時，原不等式解集為（-∞，-1）
當m>0時，原不等式的解集為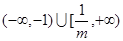
當 1<m<0時，原不等式的解集為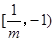
當 m=-1時，原不等式的解集為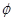
當m<-1時，原不等式的解集為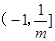
考點：1．分式不等式的解法；2．分類討論思想．
課堂練加測系列答案
輕松課堂單元測試AB卷系列答案科目：高中數學 來源： 題型：解答題
設二次函數f(x)＝ax2＋bx＋c，函數F(x)＝f(x)－x的兩個零點為m，n(m<n)．
(1)若m＝－1，n＝2，求不等式F(x)>0的解集；
(2)若a>0，且0<x<m<n<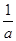
，比較f(x)與m的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知不等式(2＋x)(3－x)≥0的解集為A，函數f(x)＝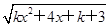
(k<0)的定義域為B.
(1)求集合A；
(2)若集合B中僅有一個元素，試求實數k的值；
(3)若B?A，試求實數k的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的解集為
，則實數a的取值范圍是 
．
時，求不等式
的解集；
存在實數解，求實數
的取值范圍.
＋1.
.
時，解不等式
；
時，
，求a的取值范圍.
．
的解集為
，求實數a的值； 
使
成立，求實數
的取值范圍． 
其中
.