
設有關于x的一元二次方程x2+2ax+b2="0." (l)若a是從0,1,2,3四個數中任取的一個數,b是從0,1,2三個數中任取的一個數,求方程有實根的概率;(2)若a是從區間[0,t+1]任取的一個數,b是從區間[0,t]任取的一個數,其中t滿足2≤t≤3,求方程有實根的概率,并求出其概率的最大值.
(1)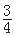 ;(2)
;(2)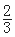 .
.
解析試題分析:(1)本小題為古典概型求概率的問題,先求出a與b構成的實數對(a,b)總個數即基本事件的總數,再一一進行檢驗符合 的實數對即可求出其概率;(2)本小題為幾何概型求概率的問題,由0≤a≤t+1,0≤b≤t利用線性規劃的知識(a看直角坐標系中的x,b看成直角坐標系中的y)可畫出如下圖的矩形,又a≥b(即為y≤x區域)則符合條件的陰影部分區域為梯形,因此所求的概率為
的實數對即可求出其概率;(2)本小題為幾何概型求概率的問題,由0≤a≤t+1,0≤b≤t利用線性規劃的知識(a看直角坐標系中的x,b看成直角坐標系中的y)可畫出如下圖的矩形,又a≥b(即為y≤x區域)則符合條件的陰影部分區域為梯形,因此所求的概率為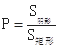 ,其次根據t的范圍利用不等式的性質求出P的范圍即可找到其最大值.
,其次根據t的范圍利用不等式的性質求出P的范圍即可找到其最大值.
試題解析:(1)總的基本事件有12個,即a,b構成的實數對(a,b)有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).設事件A為“方程有實根”,包含的基本事件有(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9個,所以事件A的概率為P(A)=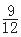 =
=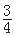 ;
;
(2)a,b構成的實數對(a,b)滿足條件有0≤a≤t+1,0≤b≤t,a≥b,設事件B為“方程有實根”,則此事件滿足幾何概型. 如圖,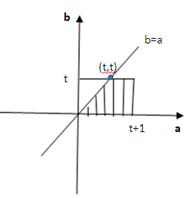
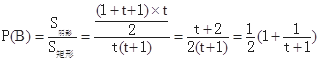 ,∵2≤t≤3,∴3≤t+1≤4,即
,∵2≤t≤3,∴3≤t+1≤4,即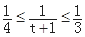 ,所以
,所以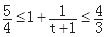 ,即
,即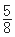 ≤P(B)≤
≤P(B)≤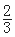 ,所以其概率的最大值為
,所以其概率的最大值為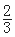 .
.
考點:古典概型的概率公式,幾何概型的概率公式,一元二次方程根的判別式,線性規劃問題,不等式的性質,化歸思想.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
某企業主要生產甲、乙兩種品牌的空調,由于受到空調在保修期內維修費等因素的影響,企業生產每臺空調的利潤與該空調首次出現故障的時間有關,甲、乙兩種品牌空調的保修期均為3年,現從該廠已售出的兩種品牌空調中各隨機抽取50臺,統計數據如下:
| 品牌 | 甲 | 乙 | |||||
| 首次出現故障時間 x年 |  |  |  |  |  |  |  |
| 空調數量(臺) | 1 | 2 | 4 | 43 | 2 | 3 | 45 |
| 每臺利潤(千元) | 1 | 2 | 2.5 | 2.7 | 1.5 | 2.6 | 2.8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某縣為增強市民的環境保護意識,面向全縣征召義務宣傳志愿者,先從符合條件的志愿者中隨機抽取100名按年齡分組:第1組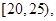 第2組
第2組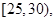 第3組
第3組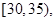 第4組
第4組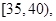 第5組
第5組 得到的頻率分布直方圖如圖所示,
得到的頻率分布直方圖如圖所示,
(1)分別求第3,4,5組的頻率。
(2)若從第3,4,5組中用分層抽樣的方法抽取6名志愿者參與廣場的宣傳活動,應從第3,4,5組各抽取多少名志愿者.
(3)在(2)的條件下,該縣決定在這6名志愿者中隨機抽取2名志愿者介紹宣傳經驗,求第4組至少有一名志愿者被抽中的概率.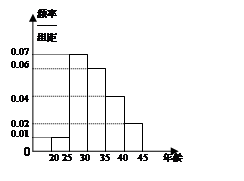
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
甲、乙兩人各進行3次射擊,甲每次擊中目標的概率為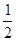 ,乙每次擊中目標的概率
,乙每次擊中目標的概率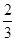 .
.
(1)記甲擊中目標的次數為ξ,求ξ的概率分布列及數學期望Eξ;
(2)求甲恰好比乙多擊中目標2次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2008年5月12日,四川汶川發生8.0級特大地震,通往災區的道路全部中斷. 5月12日晚,抗震救災指揮部決定從水路(一支隊伍)、陸路(東南和西北兩個方向各一支隊伍)和空中(一支隊伍)同時向災區挺進.在5月13日,仍時有較強余震發生,天氣狀況也不利于空中航行. 已知當天從水路抵達災區的概率是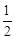 ,從陸路每個方向抵達災區的概率都是
,從陸路每個方向抵達災區的概率都是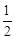 ,從空中抵達災區的概率是
,從空中抵達災區的概率是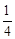 .
.
(1)求在5月13日恰有1支隊伍抵達災區的概率;
(2)求在5月13日抵達災區的隊伍數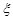 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某校學生的視力情況,現采用隨機抽樣的方式從該校的A,B兩班中各抽5名學生進行視力檢測.檢測的數據如下:
A班5名學生的視力檢測結果:4.3,5.1,4.6,4.1,4.9.
B班5名學生的視力檢測結果:5.1,4.9,4.0,4.0,4.5.
(1)分別計算兩組數據的平均數,從計算結果看,哪個班的學生視力較好?;
(2)由數據判斷哪個班的5名學生視力方差較大?(結論不要求證明)
(3)根據數據推斷A班全班40名學生中有幾名學生的視力大于4.6?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某保險公司利用簡單隨機抽樣方法,對投保車輛進行抽樣,樣本車輛中每輛車的賠付結果統計如下:
| 賠付金額(元) | 0 | 1000 | 2000 | 3000 | 4000 |
| 車輛數(輛) | 500 | 130 | 100 | 150 | 120 |
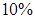 ,在賠付金額為4000元的樣本車輛中,車主是新司機的占
,在賠付金額為4000元的樣本車輛中,車主是新司機的占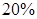 ,(3)估計在已投保車輛中,新司機獲賠金額為4000元的概率.
,(3)估計在已投保車輛中,新司機獲賠金額為4000元的概率.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com