如圖,已知四邊形ABCD內(nèi)接于
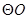
,且AB是的
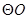
直徑,過點D的
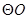
的切線與BA的延長線交于點M.

(1)若MD=6,MB=12,求AB的長;
(2)若AM=AD,求∠DCB的大小.
(1)
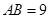
;(2)
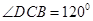
.
試題分析:本題主要以圓為幾何背景考查角的關系和邊的關系,可以運用切割線定理、弦切角定理等數(shù)學知識來證明.第一問,先利用切割線定理得到
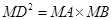
,將已知條件代入,得到
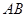
的長;第二問,因為
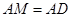
,所以
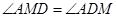
,由弦切角定理得
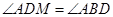
,因為
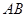
為直徑,所以
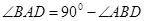
,而
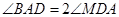
,所以
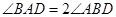
,所以
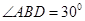
,所以
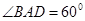
,由于
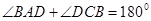
,所以
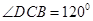
.
試題解析:(1)因為
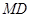
為
的切線,由切割線定理知,
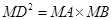
,又
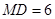
,
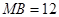
,
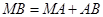
,
所以
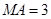
,
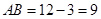
. 5分
(2)因為
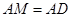
,所以
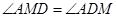
,連接
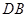
,又
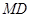
為
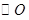
的切線,
由弦切角定理知,
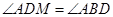
, 7分
又因為
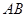
是
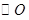
的直徑,所以
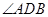
為直角,即
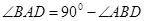
.
又
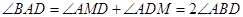
,于是
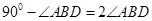
,所以
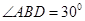
,
所以
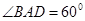
. 8分
又四邊形
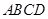
是圓內(nèi)接四邊形,所以
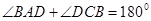
,
所以
10分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線AD交⊙O于點D,DE⊥AC,交AC的延長線于點E,OE交AD于點F.
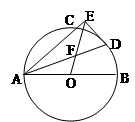
(I)求證:DE是⊙O的切線;
(II)若
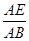
=
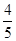
,求
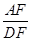
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖所示,在⊙O中,已知∠ACB=∠CDB=60°,AC=3,則△ABC的周長是________.
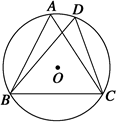
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,已知
PA,
PB是圓
O的切線,
A,
B分別為切點,
C為圓
O上不與
A,
B重合的另一點,若∠
ACB=120°,則∠
APB=________.
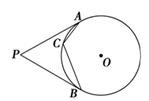
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
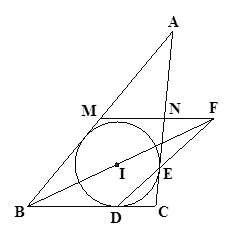
如圖,

的內(nèi)心為
,
分別是

的中點,
,內(nèi)切圓
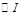
分別與邊
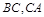
相切于
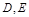
;證明:
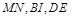
三線共點.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
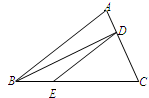
已知
的面積為1,點
在
上,
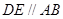
,連結
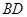
,設
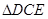
、
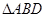
、
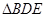
中面積最大者的值為
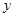
,則
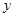
的最小值為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
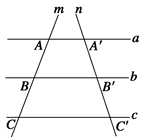
如圖所示,已知a∥b∥c,直線m、n分別與a、b、c交于點A、B、C和A′、B′、C′,如果AB=BC=1,A′B′=
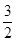
,則B′C′=________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,圓
的割線
交圓
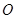
于
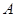
、
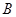
兩點,割線
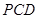
經(jīng)過圓心.已知
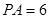
,
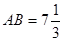
,
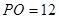
.則圓
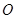
的半徑
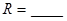
.
查看答案和解析>>

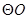 ,且AB是的
,且AB是的 直徑,過點D的
直徑,過點D的 的切線與BA的延長線交于點M.
的切線與BA的延長線交于點M.
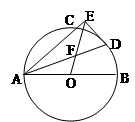
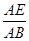 =
=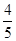 ,求
,求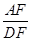 的值.
的值.
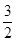 ,則B′C′=________.
,則B′C′=________.