
在四棱錐P-ABCD中,AB∥DC,AB⊥平面PAD, PD=AD,AB=2DC,E是PB的中點.
求證:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB.
(1)詳見解析; (2)詳見解析.
解析試題分析:(1)要證明線面平行根據線面平行的判定定理可將問題轉化為證明平面外直線平行與平面內一條直線,則此問題關鍵即為找出這條直線,又由題中所給:AB=2DC,E是PB的中點,不難想到取PA的中點,進而運用三角形的中位線構造平行關系,問題即可得證; (2)中要證明面面垂直由面面垂直的判定定理可知將問題轉化為證明線面垂直,結全題中所給條件和(1)中已證明的過程,不難發現可轉化為去證: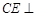 平面PAB,再根據線面垂直的判定定理可轉化為證線線垂直:
平面PAB,再根據線面垂直的判定定理可轉化為證線線垂直: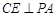 ,
,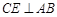 ,這樣問題即可得證.
,這樣問題即可得證.
試題解析:(1)取PA的中點F,連EF,DF. 2分
因為E是PB的中點,所以EF // AB,且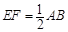 .
.
因為AB∥CD,AB=2DC,所以EF∥CD, 4分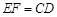 ,于是四邊形DCEF是平行四邊形,
,于是四邊形DCEF是平行四邊形,
從而CE∥DF,而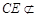 平面PAD,
平面PAD,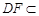 平面PAD,
平面PAD,
故CE∥平面PAD. 7分
(2)因為PD=AD,且F是PA的中點,所以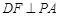 .
.
因為AB⊥平面PAD,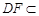 平面PAD,所以
平面PAD,所以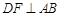 . 10分
. 10分
因為CE∥DF,所以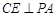 ,
,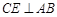 .
.
因為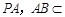 平面PAB,
平面PAB,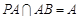 ,所以
,所以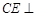 平面PAB.
平面PAB.
因為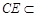 平面PBC,所以平面PBC⊥平面PAB. 14分
平面PBC,所以平面PBC⊥平面PAB. 14分
考點:1.線線,線面平行的轉化;2.線線,線面,面面垂直的轉化


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P—ABCD中,側面PAD是正三角形,且垂直于底面ABCD,底面ABCD是邊長為2的菱形,∠BAD=60°,M為PC的中點.
(1)求證:PA//平面BDM;
(2)求直線AC與平面ADM所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)已知四棱錐P—GBCD中(如圖),PG⊥平面GBCD,GD∥BC,GD=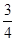 BC,且BG⊥GC,GB=GC=2,E是BC的中點,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中點,PG=4
(Ⅰ)求異面直線GE與PC所成角的余弦值;
(Ⅱ)若F點是棱PC上一點,且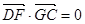 ,
,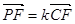 ,求
,求 的值.
的值.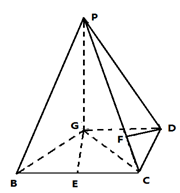
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,點D在棱AB上.
(1)求證:AC⊥B1C;
(2)若D是AB中點,求證:AC1∥平面B1CD.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱錐P-ABCD中,底面ABCD為菱形,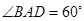 ,Q為AD的中點.
,Q為AD的中點.

(1)若PA=PD,求證:平面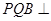 平面PAD;
平面PAD;
(2)點M在線段上,PM=tPC,試確定實數t的值,使PA//平面MQB.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在四棱柱 中,
中, 底面
底面 ,底面
,底面 為菱形,
為菱形, 為
為 與
與 交點,已知
交點,已知 ,
, .
.
(1)求證: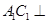 平面
平面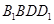 ;
;
(2)求證: ∥平面
∥平面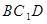 ;
;
(3)設點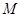 在
在 內(含邊界),且
內(含邊界),且
 ,說明滿足條件的點
,說明滿足條件的點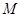 的軌跡,并求
的軌跡,并求 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com