
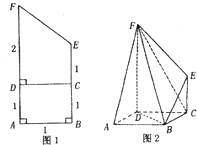
 將如圖1的直角梯形ABEF(圖中數字表示對應線段的長度)沿直線CD折成直二面角,連接部分線段后圍成一個空間幾何體,如圖2所示.
將如圖1的直角梯形ABEF(圖中數字表示對應線段的長度)沿直線CD折成直二面角,連接部分線段后圍成一個空間幾何體,如圖2所示. (I)證明:取DF的中點為G,連接AG,EG,
(I)證明:取DF的中點為G,連接AG,EG, CD
CD AB,
AB, ,且F-DC-A為直二面角,
,且F-DC-A為直二面角,
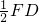 ,
,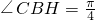 ,
, ,DF=2,BD=
,DF=2,BD= ,
, =
=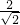 =
= ,
, .
. CD
CD AB,所以四邊形ABEG為平行四邊形,由此能夠證明BE∥平面ADF.
AB,所以四邊形ABEG為平行四邊形,由此能夠證明BE∥平面ADF. ,且F-DC-A為直二面角,知FD⊥平面ABCD,故FD⊥BH,又CE
,且F-DC-A為直二面角,知FD⊥平面ABCD,故FD⊥BH,又CE
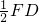 ,所以在Rt△BCH中,
,所以在Rt△BCH中,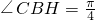 ,由此能夠求出平面FBE與平面ABCD所成角的正切值.
,由此能夠求出平面FBE與平面ABCD所成角的正切值.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
 如圖,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,AB=2,E為AB的中點,將△ADE沿DE翻折至△A′DE,使二面角A′-DE-B為直二面角.
如圖,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,AB=2,E為AB的中點,將△ADE沿DE翻折至△A′DE,使二面角A′-DE-B為直二面角.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.點E、F分別是PC、BD的中點,現將△PDC沿CD折起,使PD⊥平面ABCD,
如圖,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.點E、F分別是PC、BD的中點,現將△PDC沿CD折起,使PD⊥平面ABCD,查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
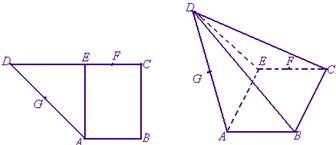 如圖,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
如圖,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com