中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

在直角坐標系xOy中,橢圓C1: =1 (a＞b＞0)的左、右焦點分別為F1、F2.F2也是拋物線C2：y2=4x的焦點，點M為C1與C2在第一象限的交點，且|MF2|=.

（1）求C1的方程；

（2）平面上的點N滿足=+，直線l∥MN，且與C1交于A、B兩點，若·=0，求直線l的方程.

（1）（2）直線l的方程為y=x-2,或y=x+2


解析:

(1)由C2:y2=4x,知F2(1,0),

設M(x1,y1),M在C2上,

因為|MF2|=,所以x1+1=,

得x1=,y1=.所以M.

M在C1上,且橢圓C1的半焦距c=1,

于是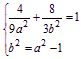

消去b2并整理得9a4-37a2+4=0.

解得a=2(a=不合題意,舍去).

故b2=4-1=3.

故橢圓C1的方程為.

(2)由=+,知四邊形MF1NF2是平行四邊形,其中心為坐標原點O,

因為l∥MN,所以l與OM的斜率相同.

故l的斜率k==.

設l的方程為y=(x-m).

由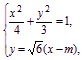消去y并整理得

9x2-16mx+8m2-4=0.

設A(x1,y1),B(x2,y2),

則x1+x2=,x1x2=.

因為⊥,所以x1x2+y1y2=0.

所以x1x2+y1y2=x1x2+6(x1-m)(x2-m)

=7x1x2-6m(x1+x2)+6m2

=7·-6m·+6m2=(14m2-28)=0.

所以m=±.此時Δ=(16m)2-4×9(8m2-4)＞0.

故所求直線l的方程為y=x-2,或y=x+2.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

在直角坐標系xOy中，橢圓C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦點分別為F1，F2．F2也是拋物線C2：y2=4x的焦點，點M為C1與C2在第一象限的交點，且|MF2|=
5
3
．
（Ⅰ）求C1的方程；
（Ⅱ）平面上的點N滿足
MN
=
MF1
+
MF2
，直線l∥MN，且與C1交于A，B兩點，若
OA
•
OB
=0，求直線l的方程．

查看答案和解析>>

科目：高中數學 來源： 題型：

在直角坐標系xOy中，已知點P（2cosx+1，2cos2x+2）和點Q（cosx，-1），其中x∈[0，π]．若向量
OP
與
OQ
垂直，求x的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

精英家教網如圖所示，在直角坐標系xOy中，射線OA在第一象限，且與x軸的正半軸成定角60°，動點P在射線OA上運動，動點Q在y軸的正半軸上運動，△POQ的面積為2
3
．
（1）求線段PQ中點M的軌跡C的方程；
（2）R1，R2是曲線C上的動點，R1，R2到y軸的距離之和為1，設u為R1，R2到x軸的距離之積．問：是否存在最大的常數m，使u≥m恒成立？若存在，求出這個m的值；若不存在，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

在直角坐標系xOy中，已知圓M的方程為x2+y2-4xcosα-2ysinα+3cos2α=0（α為參數），直線l的參數方程為
x=tcosθ
y=1+tsinθ
(t為參數）
（I）求圓M的圓心的軌跡C的參數方程，并說明它表示什么曲線；
（II）求直線l被軌跡C截得的最大弦長．

查看答案和解析>>

科目：高中數學 來源： 題型：

在直角坐標系xOy中，已知橢圓C：
x2
a2
+
y2
b2
=1(a＞b＞0)的離心率e=
2
2
，左右兩個焦分別為F1，F2．過右焦點F2且與x軸垂直的直線與橢圓C相交M、N兩點，且|MN|=2．
（1）求橢圓C的方程；
（2）設橢圓C的一個頂點為B（0，-b），是否存在直線l：y=x+m，使點B關于直線l 的對稱點落在橢圓C上，若存在，求出直線l的方程，若不存在，請說明理由．

查看答案和解析>>

同步練習冊答案