
甲、乙、丙三人獨立破譯同一份密碼,已知甲、乙、丙各自破譯出密碼的概率分別為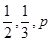 .且他們是否破譯出密碼互不影響.若三人中只有甲破譯出密碼的概率為
.且他們是否破譯出密碼互不影響.若三人中只有甲破譯出密碼的概率為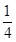 .
.
(Ⅰ)求甲乙二人中至少有一人破譯出密碼的概率;
(Ⅱ)求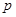 的值;
的值;
(Ⅲ)設甲、乙、丙三人中破譯出密碼的人數為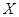 ,求
,求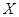 的分布列和數學期望
的分布列和數學期望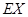 .
.
(1)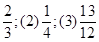 .
.
【解析】(2)可以利用對立事件來做:那就是先求出甲乙二人都沒有破譯出密碼的概率,然后利用相互對立事件的概率和為1求解.
(2)根據三人中只有甲破譯出密碼的概率為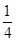 ,可求出丙獨自破譯出密碼的概率p.
,可求出丙獨自破譯出密碼的概率p.
(3)X的可能值不能搞錯:有0,1,2,3.然后分別求出其概率,求出分布列,再利用期望公式求解即可.
解:記“甲、乙、丙三人各自破譯出密碼”分別為事件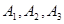 ,依題意有
,依題意有
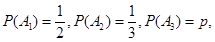 且
且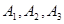 相互獨立.
相互獨立.
(Ⅰ)甲、乙二人中至少有一人破譯出密碼的概率為 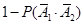
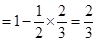 .
.
(Ⅱ)設“三人中只有甲破譯出密碼”為事件 ,則有
,則有
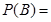
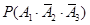 =
=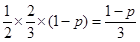 , 所以
, 所以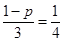 ,
,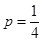 .
.
(Ⅲ)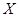 的所有可能取值為
的所有可能取值為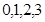 . 所以
. 所以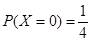 ,
,
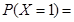
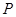
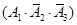
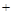
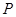
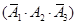
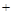
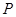
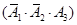
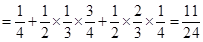 ,
,
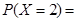
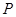
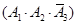
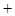
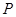
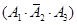
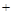
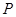
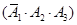
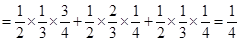 ,
,
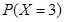 =
=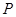
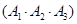 =
=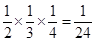 .
.
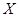 分布列為:
分布列為:
|
|
|
|
|
|
|
|
|
|
|
|
所以,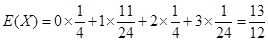 .
.


科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2014屆內蒙古赤峰市高三摸底考試理科數學試卷(解析版) 題型:解答題
甲、乙、丙三人獨立破譯同一份密碼,已知甲、乙、丙各自破譯出密碼的概率分別為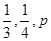 ,
,
且他們是否破譯出密碼互不影響,若三人中只有甲破譯出密碼的概率為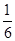 .
.
(1)求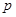 的值,
的值,
(2)設在甲、乙、丙三人中破譯出密碼的總人數為X,求X的分布列和數學期望E(X).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com