

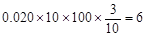



 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數學 來源:不詳 題型:解答題
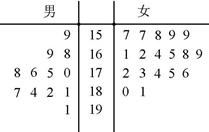
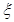 表示所選代表中女“運動健將”的人數,試寫出
表示所選代表中女“運動健將”的人數,試寫出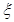 的分布列,并求
的分布列,并求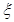 的數學期望.
的數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 元獎金.假設顧客每次抽獎時獲獎與否的概率都是
元獎金.假設顧客每次抽獎時獲獎與否的概率都是 ,
, 元的概率;
元的概率; .請寫出
.請寫出 的分布列,并求
的分布列,并求 的數學期望;
的數學期望;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 動作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | 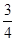 | 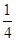 | 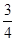 | 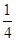 |
| 動作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | 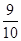 | 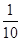 | 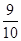 | 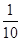 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 分.
分. 的分布列及數學期望.
的分布列及數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com