
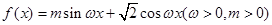 的最大值為
的最大值為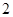 ,且
,且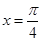 ,
,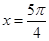 是相鄰的兩對稱軸方程.
是相鄰的兩對稱軸方程.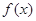 在
在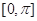 上的值域;
上的值域;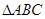 中,
中,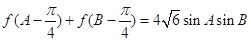 ,角
,角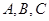 所對的邊分別是
所對的邊分別是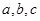 ,且
,且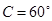 ,
,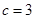 ,求
,求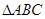 的面積.
的面積. 在
在 上的值域為
上的值域為 ;(2)
;(2)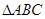 的面積為
的面積為 .
. 的最大值為
的最大值為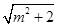 列式解出
列式解出 的值,并將函數(shù)
的值,并將函數(shù) 的解析式化為
的解析式化為 的形式,根據(jù)三角函數(shù)兩條相鄰對稱軸之間的距離與周期的關(guān)系,求出函數(shù)
的形式,根據(jù)三角函數(shù)兩條相鄰對稱軸之間的距離與周期的關(guān)系,求出函數(shù) 的最小正周期,進而求出
的最小正周期,進而求出 的值,然后再由
的值,然后再由 ,確定出
,確定出 的取值范圍,然后結(jié)合函數(shù)
的取值范圍,然后結(jié)合函數(shù) 的圖象確定函數(shù)
的圖象確定函數(shù) 的值域;(2)先利用正弦定理求出
的值域;(2)先利用正弦定理求出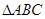 的外接圓的半徑,然后利用正弦定理中的邊角互化的思想并結(jié)合題中的等式將
的外接圓的半徑,然后利用正弦定理中的邊角互化的思想并結(jié)合題中的等式將 與
與 所滿足的等式確定下來,再利用余弦定理求出
所滿足的等式確定下來,再利用余弦定理求出 的值求出來,最后再利用三角形的面積公式
的值求出來,最后再利用三角形的面積公式 即可算出
即可算出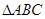 的面積.
的面積. 的最大值為
的最大值為 ,所以
,所以 .
.  ,于是
,于是 ,
, . ∵
. ∵ 是相鄰的兩對稱軸方程.
是相鄰的兩對稱軸方程. , ∴ω=1
, ∴ω=1 ,∵
,∵
 的值域為
的值域為 .
. ,由題意,得
,由題意,得 .
.  ,得
,得 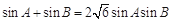 .
. 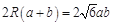 ,
,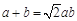 . ①
. ① ,即
,即 . ②
. ② .
.  ,或
,或  (舍去).
(舍去). 
 .
. 

 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
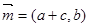 ,
,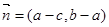 ,且
,且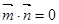 ,其中A、B、C是
,其中A、B、C是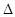 ABC的內(nèi)角,
ABC的內(nèi)角,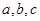 分別是角A,B,C的對邊。
分別是角A,B,C的對邊。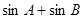 的取值范圍;
的取值范圍;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
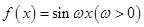 在區(qū)間
在區(qū)間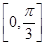 上單調(diào)遞增,在區(qū)間
上單調(diào)遞增,在區(qū)間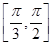 上單調(diào)遞減,則
上單調(diào)遞減,則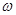 =( )
=( )| A.3 | B.2 | C.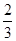 | D.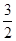 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
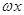 +ACos
+ACos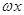 (
(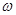 >0)的圖像關(guān)于M(
>0)的圖像關(guān)于M(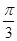 ,0)對稱,且在
,0)對稱,且在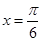 處函數(shù)有最小值,則
處函數(shù)有最小值,則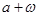 的一個可能取值是( )
的一個可能取值是( ) | A.0 | B.3 | C.6 | D.9 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com