
(Ⅰ)寫出xn與x n-1、x n-2之間的關系式(n≥3);
(Ⅱ)設an=x n+1-xn,計算a1,a2,a3,由此推測數列{an}的通項公式,并加以證明;
(Ⅲ)求![]() xn.
xn.
(21)本題主要考查直線與橢圓等基礎知識,考查綜合運用數學知識和方法分析解決問題的能力.
(Ⅰ)解:當n≥3時,xn=![]() .
.
(Ⅱ)解:a1=x2-x1=a,
a2=x3-x2=![]() -x2=-
-x2=-![]() (x2-x1)=-
(x2-x1)=-![]() a,
a,
a3=x4-x3=![]() -x3=-
-x3=-![]() (x3-x2)=-
(x3-x2)=-![]() (-
(-![]() a)=
a)=![]() (a)
(a)
由此推測an=(-![]() )n-
)n-
證法一:
因為a1=a>0,且an=xn+1-xn=![]() -xn=
-xn=![]() =-
=-![]() (xn-xn-1)=-
(xn-xn-1)=-![]() an-1
an-1
(n≥2),
所以an=(-![]() )n-1(a)
)n-1(a)
證法二:
用數學歸納法證明:
(i)當n=1時,a1=x2-x1=a=(![]() )
)
(ii)假設當n=k時,公式成立,即ak=(![]() )k-
)k-
那么當n=k+1時,
ak+1=xk+2-xk+1=![]() -xk+1=-
-xk+1=-![]() (xk+1-xk)=-
(xk+1-xk)=-![]() ak=-
ak=-![]() (-
(-![]() )k-
)k-
=(-![]() )(k+1)-
)(k+1)-
根據(i)與(ii)可知,對任意n∈N,公式an=(-![]() )n-
)n-
(Ⅲ)解:當n≥3時,有
xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1=an-1+an-2+…+a1,
由(Ⅱ)知{an}是公比為-![]() 的等比數列,
的等比數列,
所以![]() xn=
xn=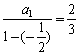 (a).
(a).


科目:高中數學 來源: 題型:
(Ⅰ)寫出xn與x n-1、x n-2之間的關系式(n≥3);
(Ⅱ)設an=x n+1-xn,計算a1,a2,a3,由此推測數列{an}的通項公式,并加以證明;
(Ⅲ)求![]() xn.
xn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com