
已知圓 ,過點
,過點 作直線交圓C于
作直線交圓C于 兩點,
兩點, 面積的最大值為__________.
面積的最大值為__________.
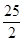
解析試題分析:根據(jù)題意可設(shè)出過點M(1,3)的直線l方程,利用點到直線的距離公式求得圓心(4,0)到l的距離,用弦心距、半弦長、半徑組成的直角三角形進(jìn)行計算轉(zhuǎn)化,從而可得到△ABC面積的表達(dá)式,可求得其最大值. 設(shè)過點M(1,3)的直線方程為l:y-3=k(x-1),由x2-8x+y2-9=0得圓心C(4,0),半徑r=5,設(shè)圓心C(4,0)到直線l的距離為d,點C在l上的射影為M,則d=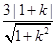 ,ABC
,ABC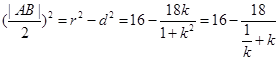 ,然后根據(jù)均值不等式得到了三角形面積的
,然后根據(jù)均值不等式得到了三角形面積的 為
為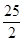
考點:直線方程與圓的方程的應(yīng)用
點評:本題考查直線方程與圓的方程的應(yīng)用,解決的方法利用弦心距、半弦長、半徑組成的直角三角形進(jìn)行計算,難點在于復(fù)雜的運算與化歸,屬于難題.


 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案科目:高中數(shù)學(xué) 來源: 題型:填空題
以點C (t,  )(t∈R , t ≠ 0)為圓心的圓過原點O,直線y = -2x-4與圓C交于點M, N, 若
)(t∈R , t ≠ 0)為圓心的圓過原點O,直線y = -2x-4與圓C交于點M, N, 若 ,則圓C的方程 .
,則圓C的方程 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
設(shè) ,若直線
,若直線 與
與 軸相交于點
軸相交于點 ,與
,與 軸相交于
軸相交于 ,且
,且 與圓
與圓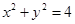 相交所得弦的長為2,
相交所得弦的長為2, 為坐標(biāo)原點,則
為坐標(biāo)原點,則 面積的最小值為_________.
面積的最小值為_________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com