
| 解:由已知,有A+B+C= ∴B= ∴tan ∵tan ∴tanA,tanC是方程 解得t=1或t= 又∵A<C,∴tanA=1,tanC= 而 ∴A= 故角A,B,C的值分別為 注:此題具有一定的綜合性,除了應具備三角形,數列及三角公式等知識外,方程思想的體現(得到以tanA,tanC為未知數的方程組)與應用也是十分關鍵的.
|
| 分析:在△ABC中,首先有A+B+C=180°,又三內角成等差數列。
∴2B=A+C,因此B=
|


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
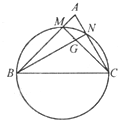 (2013•成都一模)如圖,已知在△ABC中,BC=2,以BC為直徑的圓分別交AB,AC于點M,N,MC與NB交于點G,若
(2013•成都一模)如圖,已知在△ABC中,BC=2,以BC為直徑的圓分別交AB,AC于點M,N,MC與NB交于點G,若| BM |
| BC |
| CN |
| BC |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| AP |
| AB |
| AC |
| A、為定值2 |
| B、最大值為4 |
| C、最小值為1 |
| D、與P的位置有關 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com