|
|
|
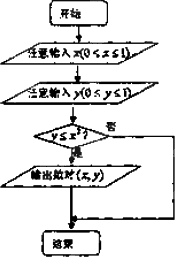
閱讀下面程序框圖,任意輸入一次x(0≤x≤1)與y(0≤y≤1),則能輸出數對(x,y)的概率為
|
| [ ] |
A. |
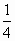
|
B. |
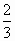
|
C. |
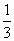
|
D. |
|
|
|
練習冊系列答案
相關習題
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
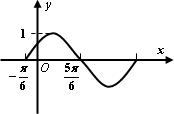
函數f(x)=Asin(ωx+φ)的圖象如圖所示,其中A>0,ω>0,|φ|< .則下列關于函數f(x)的說法中正確的是 .則下列關于函數f(x)的說法中正確的是
|
| [ ] |
A. |
對稱軸方程是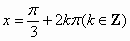
|
B. |
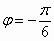
|
C. |
最小正周期是π
|
D. |
在區間 上單調遞減 上單調遞減
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
對定義在區間l,上的函數f(x),若存在開區間(a,b) I和常數C,使得對任意的x∈(a,b)都有-C<f(x)<C,且對任意的x I和常數C,使得對任意的x∈(a,b)都有-C<f(x)<C,且對任意的x (a,b)都有|f(x)|=C恒成立,則稱函數f(x)為區間I上的“Z型”函數. (a,b)都有|f(x)|=C恒成立,則稱函數f(x)為區間I上的“Z型”函數.
(Ⅰ)求證:函數f(x)=|x-3|-|x-1|是R上的“Z型”函數;
(Ⅱ)設f(x)是(I)中的“Z型”函數,若不等式|t|=|t+1|≥f(x)對任意的x∈R恒成立,求實數t的取值范圍.
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
在△ABC中,角A,B,C的對邊分別為a,b,c,已知向量m=(cosA,cosB),n=(2c+b,a),且m⊥n.
(Ⅰ)求角A的大小;
(Ⅱ)若a=4,求△ABC面積的最大值.
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
對定義在區間l,上的函數f(x),若存在開區間(a,b) I和常數C,使得對任意的x∈(a,b)都有-C<f(x)<C,且對任意的x I和常數C,使得對任意的x∈(a,b)都有-C<f(x)<C,且對任意的x (a,b)都有|f(x)|=C恒成立,則稱函數f(x)為區間Ⅰ上的“Z型”函數. (a,b)都有|f(x)|=C恒成立,則稱函數f(x)為區間Ⅰ上的“Z型”函數.
(Ⅰ)求證:函數f(x)=|x-3|-|x-1|是R上的“Z型”函數;
(Ⅱ)設f(x)是(Ⅰ)中的“Z型”函數,若不等式|t|=|t+1|≥f(x)對任意的x∈R恒成立,求實數t的取值范圍.
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
關于函數函數f(x)=2cosx(cosx+ sinx)-1,以下結論正確的是 sinx)-1,以下結論正確的是
|
| [ ] |
A. |
f(x)的最小正周期是π,在區間(- , , )是增函數 )是增函數
|
B. |
f(x)的最小正周期是π,在區間(- , , )是增函數 )是增函數
|
C. |
f(x)的最小正周期是π,最大值是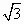
|
D. |
f(x)的最小正周期是2π,最大值是2
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
關于函數函數f(x)=2cosx(cosx+ sinx)-1,以下結論正確的是 sinx)-1,以下結論正確的是
|
| [ ] |
A. |
f(x)的最小正周期是π,在區間(- , , )是增函數 )是增函數
|
B. |
f(x)的最小正周期是π,在區間(- , , )是增函數 )是增函數
|
C. |
f(x)的最小正周期是π,最大值是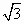
|
D. |
f(x)的最小正周期是2π,最大值是2
|
|
|
查看答案和解析>>
科目:高中數學
來源:課標綜合版 專題復習
題型:
|
|
|
在區間[0,π]內隨機取兩個數分別記為a、b,則使得函數f(x)=x2+2ax+b2+π有零點的概率為
|
| [ ] |
A. |
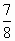
|
B. |
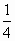
|
C. |
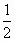
|
D. |
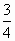
|
|
|
查看答案和解析>>

 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案