
(本題滿分15分)已知集合M={1,2,3,4,5},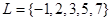 .
.
(1)用列舉法表示集合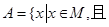
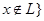 ;
;
(2)設N是M的非空真子集,且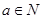 時,有
時,有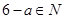 ,試寫出所有集合N;
,試寫出所有集合N;
(3)已知M的非空子集個數為31個,依次記為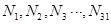 ,分別求出它們各自的元素之和,結果依次記為
,分別求出它們各自的元素之和,結果依次記為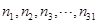 ,試計算:
,試計算: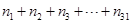 的值.
的值.
(1)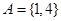 ;(2)單元子集
;(2)單元子集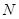 是
是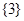 ,兩個元素的子集
,兩個元素的子集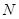 有
有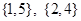
集合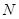 還有:
還有: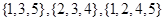 .
.
(3)在所有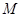 的真子集中,每個元素出現的次數均為
的真子集中,每個元素出現的次數均為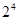
【解析】
試題分析:(1)要注意集合A中的元素是M中不屬于L的元素.顯然是L相對于M的補集.
(2)N是M的非空真子集,然后從真子集當中選出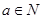 時,有
時,有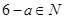 即可.據此可找出滿足條件的N有:
即可.據此可找出滿足條件的N有: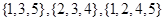
(3) 因為在所有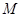 的真子集中,每個元素出現的次數均為
的真子集中,每個元素出現的次數均為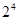 ,
,
所以所有集合中元素的和為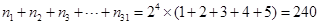 .
.
(1)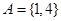 ……
……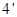
(2)單元子集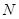 是
是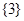 ,兩個元素的子集
,兩個元素的子集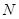 有
有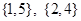 ……
……
集合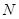 還有:
還有: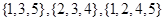 .
……
.
……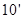
(3)在所有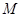 的真子集中,每個元素出現的次數均為
的真子集中,每個元素出現的次數均為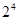
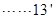
故 ……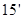 .
.
考點:集合的補運算,集合的元素的性質.
點評:本小題第(1)問實質是考查集合的補集的定義,第(2)問關鍵是搞清楚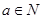 時,有
時,有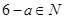 ,這個條件.第(3)知道如果集合M中有n個元素,則其非空真子集的個數為
,這個條件.第(3)知道如果集合M中有n個元素,則其非空真子集的個數為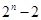 .
.


 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:高中數學 來源:2013屆浙江省余姚中學高三上學期期中考試文科數學試卷(帶解析) 題型:解答題
(本題滿分15分)已知點 (0,1),
(0,1), ,直線
,直線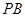 、
、 都是圓
都是圓 的切線(
的切線(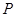 點不在
點不在 軸上).
軸上).
(Ⅰ)求過點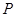 且焦點在
且焦點在 軸上的拋物線的標準方程;
軸上的拋物線的標準方程;
(Ⅱ)過點(1,0)作直線 與(Ⅰ)中的拋物線相交于
與(Ⅰ)中的拋物線相交于
 兩點,問是否存在定點
兩點,問是否存在定點 使
使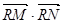 為常數?若存在,求出點
為常數?若存在,求出點 的坐標及常數;若不存在,請說明理由
的坐標及常數;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省桐鄉市高三10月月考理科數學 題型:解答題
(本題滿分15分)已知函數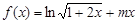 .
.
(Ⅰ)若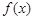 為定義域上的單調函數,求實數m的取值范圍;
為定義域上的單調函數,求實數m的取值范圍;
(Ⅱ)當 時,求函數
時,求函數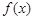 的最大值;
的最大值;
(Ⅲ)當 ,且
,且 時,證明:
時,證明: .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省桐鄉市高三下學期2月模擬考試文科數學 題型:解答題
(本題滿分15分)已知圓N: 和拋物線C:
和拋物線C: ,圓的切線
,圓的切線 與拋物線C交于不同的兩點A,B,
與拋物線C交于不同的兩點A,B,
(1)當直線 的斜率為1時,求線段AB的長;
的斜率為1時,求線段AB的長;
(2)設點M和點N關于直線 對稱,問是否存在直線
對稱,問是否存在直線 使得
使得 ?若存在,求出直線
?若存在,求出直線 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源:杭州市2010年第二次高考科目教學質量檢測 題型:解答題
(本題滿分15分)已知直線 ,曲線
,曲線
(1)若 且直線與曲線恰有三個公共點時,求實數
且直線與曲線恰有三個公共點時,求實數 的取值;
的取值;
(2)若 ,直線與曲線M的交點依次為A,B,C,D四點,求|AB+|CD|的取值范圍。[來源:Z+xx+k.Com]
,直線與曲線M的交點依次為A,B,C,D四點,求|AB+|CD|的取值范圍。[來源:Z+xx+k.Com]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com