
關于線性回歸,以下說法錯誤的是( )
(A)自變量取值一定時,因變量的取值帶有一定隨機性的兩個變量之間的關系叫做相關關系
(B)在平面直角坐標系中用描點的方法得到的表示具有相關關系的兩個變量的一組數(shù)據(jù)的圖形叫做散點圖
(C)線性回歸直線方程最能代表觀測值x,y之間的關系,且其回歸直線一定過樣本中心點(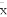 ,
,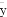 )
)
(D)甲、乙、丙、丁四位同學各自對A,B兩變量的線性相關性作試驗,并由回歸分析法分別求得相關系數(shù)rxy如下表
| 甲 | 乙 | 丙 | 丁 |
rxy | 0.82 | 0.78 | 0.69 | 0.85 |
則甲同學的試驗結果體現(xiàn)A,B兩變量更強的線性相關性
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十四選修4-2第一節(jié)練習卷(解析版) 題型:解答題
在平面直角坐標系中,一種線性變換對應的2×2矩陣為 .
.
(1)求點A( ,3)在該變換作用下的象.
,3)在該變換作用下的象.
(2)求圓x2+y2=1在該變換作用下的新曲線的方程.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十二第十章第九節(jié)練習卷(解析版) 題型:解答題
近幾年來,我國許多地區(qū)經(jīng)常出現(xiàn)干旱現(xiàn)象,為抗旱經(jīng)常要進行人工降雨.現(xiàn)由天氣預報得知,某地在未來5天的指定時間的降雨概率是:前3天均為50%,后2天均為80%,5天內(nèi)任何一天的該指定時間沒有降雨,則在當天實行人工降雨,否則,當天不實施人工降雨.
(1)求至少有1天需要人工降雨的概率.
(2)求不需要人工降雨的天數(shù)x的分布列和期望.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十九選修4-5第一節(jié)練習卷(解析版) 題型:解答題
設f(x)= x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求實數(shù)t的取值范圍.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十三第十章第十節(jié)練習卷(解析版) 題型:解答題
某班主任對全班50名學生進行了作業(yè)量多少的調(diào)查,喜歡玩電腦游戲的同學認為作業(yè)多的有18人,認為作業(yè)不多的有9人,不喜歡玩電腦游戲的同學認為作業(yè)多的有8人,認為作業(yè)不多的有15人.
(1)根據(jù)以上數(shù)據(jù)建立一個2×2的列聯(lián)表.
(2)有多大的把握認為“喜歡玩電腦游戲與認為作業(yè)多有關系”?
(參考數(shù)值: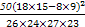 ≈5.059)
≈5.059)
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十七選修4-4第一節(jié)練習卷(解析版) 題型:解答題
在極坐標系下,已知圓O:ρ=cosθ+sinθ和直線l:ρsin(θ- )=
)= .
.
(1)求圓O和直線l的直角坐標方程.
(2)當θ∈(0,π)時,求直線l與圓O公共點的一個極坐標.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高考數(shù)學全程總復習課時提升作業(yè)七十七選修4-4第一節(jié)練習卷(解析版) 題型:解答題
求經(jīng)過極點O(0,0),A(6, ),B(6
),B(6 ,
, )三點的圓的極坐標方程.
)三點的圓的極坐標方程.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年高中數(shù)學全國各省市理科導數(shù)精選22道大題練習卷(解析版) 題型:解答題
已知函數(shù)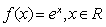 的圖象與
的圖象與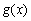 的圖象關于直線
的圖象關于直線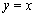 對稱。
對稱。
(Ⅰ)若直線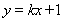 與
與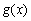 的圖像相切, 求實數(shù)
的圖像相切, 求實數(shù)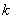 的值;
的值;
(Ⅱ)判斷曲線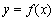 與曲線
與曲線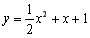 公共點的個數(shù).
公共點的個數(shù).
(Ⅲ)設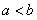 ,比較
,比較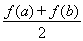 與
與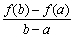 的大小, 并說明理由.
的大小, 并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源:2014年廣東省廣州市畢業(yè)班綜合測試一理科數(shù)學試卷(解析版) 題型:解答題
已知雙曲線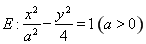 的中心為原點
的中心為原點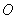 ,左、右焦點分別為
,左、右焦點分別為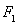 、
、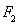 ,離心率為
,離心率為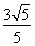 ,點
,點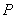 是直線
是直線 上任意一點,點
上任意一點,點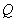 在雙曲線
在雙曲線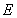 上,且滿足
上,且滿足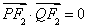 .
.
(1)求實數(shù)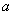 的值;
的值;
(2)證明:直線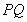 與直線
與直線 的斜率之積是定值;
的斜率之積是定值;
(3)若點 的縱坐標為
的縱坐標為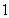 ,過點
,過點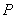 作動直線
作動直線 與雙曲線右支交于不同的兩點
與雙曲線右支交于不同的兩點 、
、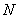 ,在線段
,在線段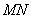 上去異于點
上去異于點 、
、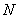 的點
的點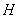 ,滿足
,滿足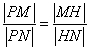 ,證明點
,證明點 恒在一條定直線上.
恒在一條定直線上.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com