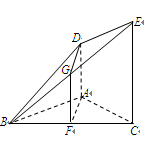
如圖,
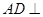
平面
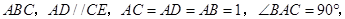
凸多面體
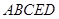
的體積為
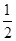
,
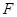
為
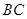
的中點.
(Ⅰ)求證:
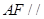
平面
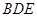
;
(Ⅱ)求證:平面
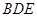
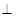
平面
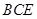
.
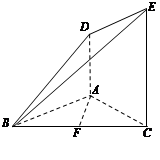
試題分析:(Ⅰ)取
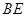
的中點G,連結
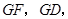
只需證明
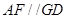
;(Ⅱ)先證明
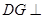
面
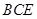
,再證平面
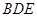
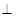
平面
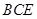
.
試題解析:(Ⅰ)證明:
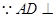
平面
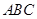
,

面
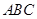
,
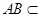
面
,

,

∴四邊形

為直角梯形. (1分)
又
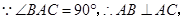
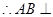
面

. (2分)
∴凸多面體
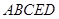
的體積
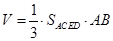
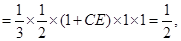
求得
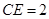
. (3分)
取
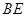
的中點G,連結
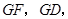
如圖:
則
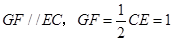
,
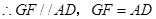
,四邊形
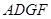
為平行四邊形,
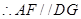
. (5分)
又∵GD

面BDE,AF
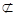
面BDE,
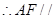
平面
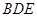
. (7分)
(Ⅱ)證明:
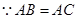
,F(xiàn)為BC的中點,
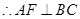
. (8分)
由(Ⅰ)知
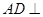
平面
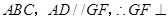
面
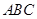
.

面
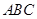
,

. (9分)
又
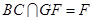
,∴
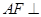
面
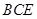
. (10分)
又∵
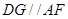
,∴
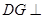
面
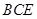
. (11分)
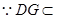
面
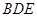
,∴面
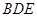
⊥面
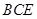
. (12分)
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
在四棱錐
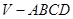
中,底面

是正方形,側面

是正三角形,平面

底面

.
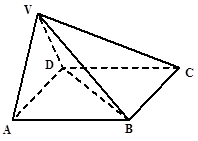
(I) 證明:

平面

;
(II)求二面角

的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
四棱錐P-ABCD中,PA⊥平面ABCD,E為AD的中點,ABCE為菱形,∠BAD=120°,PA=AB,G、F分別是線段CE、PB的中點.

(Ⅰ) 求證:FG∥平面PDC;
(Ⅱ) 求二面角

的正切值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,四邊形
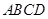
是正方形,
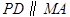
,
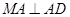
,

,
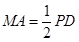
.
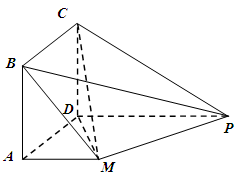
(Ⅰ)求證:平面
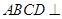
平面
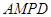
;
(Ⅱ)若
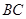
與
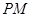
所成的角為
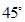
,求二面角
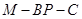
的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖1,四棱錐
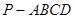
中,
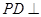
底面
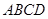
,面
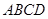
是直角梯形,

為側棱
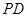
上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示.
(Ⅰ)證明:
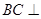
平面
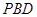
;
(Ⅱ)證明:
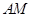
∥平面
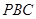
;
(Ⅲ)線段
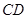
上是否存在點
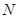
,使
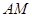
與
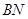
所成角的余弦值為
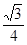
?若存在,找到所有符合要求的點
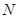
,并求
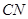
的長;若不存在,說明理由.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
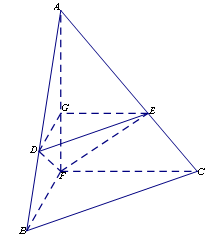
如圖,在邊長為1的等邊三角形
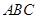
中,
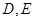
分別是
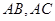
邊上的點,
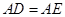
,
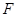
是
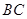
的中點,
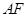
與
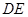
交于點
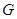
,將
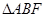
沿
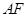
折起,得到如圖所示的三棱錐
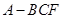
,其中
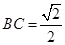
.
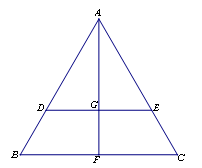
(1) 證明:
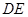
//平面
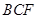
;
(2) 證明:
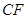
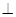
平面
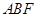
;
(3) 當
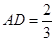
時,求三棱錐
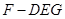
的體積
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
三棱錐S-ABC中,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=,則三棱錐外接球O的表面積等于________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖所示,三棱柱A
1B
1C
1—ABC的三視圖中,正(主)視圖和側(左)視圖是全等的矩形,俯視圖是等腰直角三角形,點M是A
1B
1的中點.
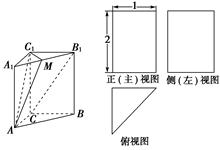
(1)求證:B
1C∥平面AC
1M;
(2)求證:平面AC
1M⊥平面AA
1B
1B.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在斜三棱柱ABC—A
1B
1C
1中,AB⊥側面BB
1C
1C,BC=2,BB
1=4,AB=
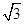
,∠BCC
1=60°.
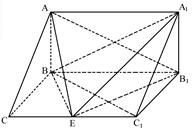
(Ⅰ)求證:C
1B⊥平面A
1B
1C
1;
(Ⅱ)求A
1B與平面ABC所成角的正切值;
(Ⅲ)若E為CC
1中點,求二面角A—EB
1—A
1的正切值.
查看答案和解析>>

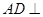 平面
平面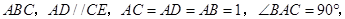 凸多面體
凸多面體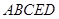 的體積為
的體積為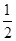 ,
,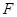 為
為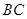 的中點.
的中點.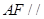 平面
平面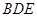 ;
;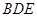
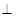 平面
平面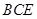 .
. 

 的正切值.
的正切值.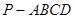 中,
中,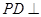 底面
底面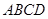 ,面
,面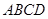 是直角梯形,
是直角梯形, 為側棱
為側棱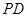 上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示.
上一點.該四棱錐的俯視圖和側(左)視圖如圖2所示. 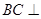 平面
平面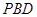 ;
; 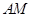 ∥平面
∥平面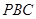 ;
; 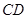 上是否存在點
上是否存在點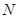 ,使
,使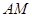 與
與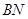 所成角的余弦值為
所成角的余弦值為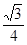 ?若存在,找到所有符合要求的點
?若存在,找到所有符合要求的點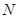 ,并求
,并求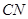 的長;若不存在,說明理由.
的長;若不存在,說明理由.
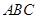 中,
中,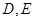 分別是
分別是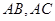 邊上的點,
邊上的點,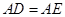 ,
,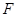 是
是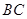 的中點,
的中點,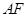 與
與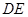 交于點
交于點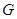 ,將
,將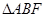 沿
沿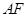 折起,得到如圖所示的三棱錐
折起,得到如圖所示的三棱錐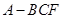 ,其中
,其中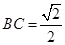 .
.

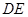 //平面
//平面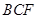 ;
;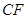
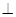 平面
平面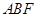 ;
;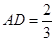 時,求三棱錐
時,求三棱錐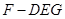 的體積
的體積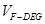 .
.
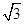 ,∠BCC1=60°.
,∠BCC1=60°.