
 B
B
 B
B 求實數a的值;
求實數a的值; B=A求實數a的取值范圍;
B=A求實數a的取值范圍;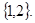
 B
B ∴2
∴2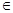 B,代入B中的方程,得a2+4a+3=0,∴a=-1或a="-3;"
B,代入B中的方程,得a2+4a+3=0,∴a=-1或a="-3;" 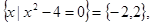 滿足條件;
滿足條件;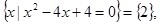 滿足條件;
滿足條件;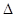 =4(a+1)2-4(a2-5)=8(a+3).
=4(a+1)2-4(a2-5)=8(a+3). B=A∴B
B=A∴B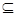 A,
A,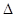 <0,即a<-3時,B=
<0,即a<-3時,B=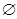 ,滿足條件;
,滿足條件;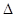 =0,即a=-3時,B=
=0,即a=-3時,B=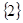 ,滿足條件;
,滿足條件;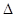 >0,即a>-3時,B=A=
>0,即a>-3時,B=A=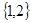 才能滿足條件, 則由根與系數的關系得
才能滿足條件, 則由根與系數的關系得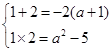 即
即 矛盾;綜上,a的取值范圍是a≤-3.
矛盾;綜上,a的取值范圍是a≤-3.

 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com