
 )有5個人并排站成一排,如果甲必須在乙的右邊,則不同的排法有
)有5個人并排站成一排,如果甲必須在乙的右邊,則不同的排法有 多少種?
多少種? 我們把3個人看成是坐在座位上的人,往5個空座的空檔插,由于這5個空座位之間共有4個空,3個人去插,共有A43=24(種).
我們把3個人看成是坐在座位上的人,往5個空座的空檔插,由于這5個空座位之間共有4個空,3個人去插,共有A43=24(種). (種),
(種),


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源:不詳 題型:單選題
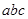 ”滿足
”滿足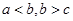 ,則這樣的三位數稱為凸數(如120,352)
,則這樣的三位數稱為凸數(如120,352)| A.240 | B.204 | C.729 | D.920 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
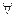 x∈R,x2 + x>0”的否定是
x∈R,x2 + x>0”的否定是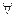 x∈R,x2 + x≤0 B
x∈R,x2 + x≤0 B 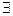 x0∈R,x02 + x0>0
x0∈R,x02 + x0>0 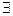 x0∈R,x02 + x0<0 D
x0∈R,x02 + x0<0 D 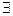 x0∈R,x02 + x0≤0
x0∈R,x02 + x0≤0查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
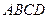 (邊長為
(邊長為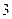 個單位)的頂點
個單位)的頂點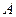 處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數為
處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數為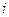 (
(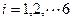 ),則棋子就按逆時針方向行走
),則棋子就按逆時針方向行走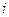 個單位,一直循環下去.則某人拋擲三次骰子后棋子恰好又回到
個單位,一直循環下去.則某人拋擲三次骰子后棋子恰好又回到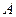 處的所有不同走法共有
處的所有不同走法共有A.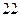 種 種 | B.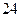 種 種 | C.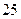 種 種 | D.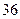 種 種 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com